Two Variable System of Equations Math Problems With Solutions

Solving the Two Variable Systems of Equations Math Problems Using Substitution

Problem 1: Solve the system of linear equations x + 2y = 8 and 3x + y = 9

Solution

Let assume

x + 2y = 8……………………………eq(1)

3x + y = 9……………………………eq(2)

From equation 1 we get

x = 8 – 2y, we can substitute the value of x in equation 2, then

3 · (8 – 2y) + y = 9

⇒ 24 – 6y + y = 9

⇒ 5y = 15

or, y = 3

Now from equation 1

x = 8 – 2y = 8 – 2 · 3 = 2

or the solution of the system of equations is x = 2 and y = 3

Problem 2: Solve the system of equations 5x + 3y = 18 and 4x + y = 13

Solution

Let assume

5x + 3y = 18………………………eq(1)

4x + y = 13………………………..eq(2)

From equation 2 we get

y = 13 – 4x, we can substitute the value of x in equation 1, then

5x + 3 · (13 – 4x) = 18

⇒ 5x + 39 – 12x = 18

⇒ 7x = 21

or, x = 3

Now from equation 2

y = 13 – 4x = 13 – 4 · 3 = 1

or the solution of the system of equations is x = 3 and y = 1

Solving the Two Variable Systems of Equations Math Problems Using Elimination

Problem 3: Solve the system of equations 4x + 3y = 31 and 3x + 2y = 22

Solution

Let assume

4x + 3y = 31………………………..eq(1)

3x + 2y = 22………………………..eq(2)

Multiply equation 1 with 2 and equation 2 with 3, then the coefficient of y becomes 6

2 · (4x + 3y) = 2 · 31

⇒ 8x + 6y = 62………………………..eq(3)

3 · (3x + 2y) = 3 · 22

⇒ 9x + 6y = 66………………………..eq(4)

Now we can eliminate y by subtracting equation 3 from equation 4

9x + 6y – (8x + 6y) = 66 – 62

⇒ x = 4

From equation 1, we get

4 · 4 + 3y = 31

⇒ 3y = 31 – 16 = 15

⇒ y = 5

or the solution of the system of equations is x = 4 and y = 5

Problem 4: Solve the system of equations 5x + 6y = 28 and 3x + 5y = 21

Solution

Let assume

5x + 6y = 28………………………..eq(1)

3x + 5y = 21………………………..eq(2)

Multiply equation 1 with 3 and equation 2 with 5, then the coefficient of x becomes 15

3 · (5x + 6y) = 3 · 28

⇒ 15x + 18y = 84………………………..eq(3)

5 · (3x + 5y) = 5 · 21

⇒ 15x + 25y = 105………………………..eq(4)

Now we can eliminate x by subtracting equation 3 from equation 4

15x + 25y – (15x + 18y) = 105 – 84

⇒ 7y = 21

⇒ y = 3

From equation 1, we get

5x + 6 · 3 = 28

⇒ 5x = 28 – 18 = 10

⇒ x = 2

or the solution of the system of equations is x = 2 and y = 3

Solving the Two Variable Systems of Equations Math Problems Using Graphs

Problem 5: Solve the system of equations x + 2y = 5 and x – 2y = 1

Solution

We will plot the graphs of x + 2y = 5 and x – 2y = 1 to solve the equation

Here x + 2y = 5 and x – 2y = 1 intersecting at (3, 2) so the solution of the system of equation is x = 3 and y = 2

Problem 6: Solve the system of equations 3x + y = 8 and 2x – 3y = -2

Solution

We will plot the graphs of 3x + y = 8 and 2x – 3y = -2 to solve the equation

Here 3x + y = 8 and 2x – 3y = -2 intersecting at (2, 2) so the solution of the system of equation is x = 2 and y = 2

Solving the Two Variable Systems of Equations Math Problems Using Matrices

Problem 7: Solve the system of equations 2x + 3y = 1 and 6x + y = 11

Solution

Here coefficient matrix (A), variable matrix (X), and constant matrix (B) is

We know  X = A⁻¹B, so

Now we get

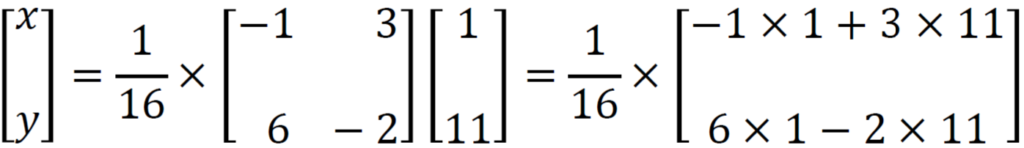
Simplify this, then we get

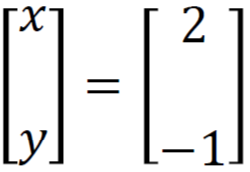
So the solutions are x = 2 and y = -1

Problem 8: Solve the system of equations 3x + y = 1 and x + 2y = -3

Solution

Here coefficient matrix (A), variable matrix (X), and constant matrix (B) is

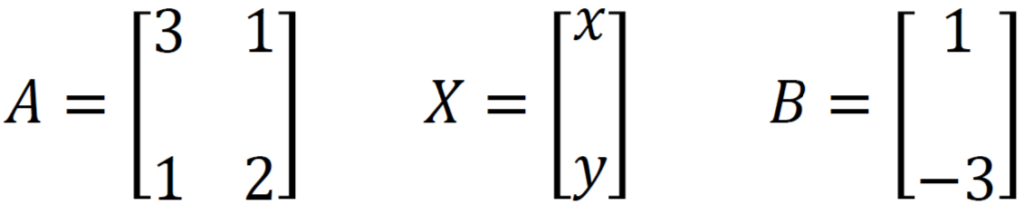
We know  X = A⁻¹B, so

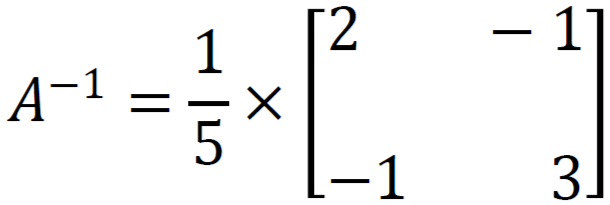
Now we get

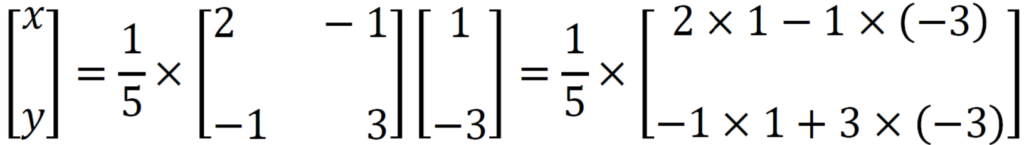
Simplify this, then we get

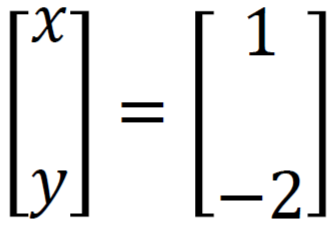
So the solutions are x = 1 and y = -2