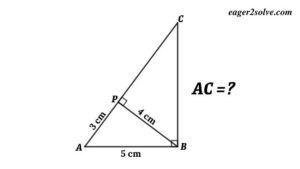
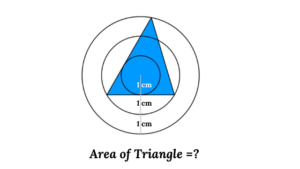
In this blog, we are discussing 5 trigonometry math problems with triangles and their solutions using trigonometry which include several properties of triangles like cosine rule, sine rule, projection formula, etc
Problem 1: Radius of the Circumcircle of the Triangle
Trigonometry Math Problems with Triangles 1: Find the radius of the circumcircle of the triangle
Triangle ABC’s sides are AB = 9 cm, BC = 8 cm, and AC = 6 cm. Then find the radius of the circumcircle of the triangle
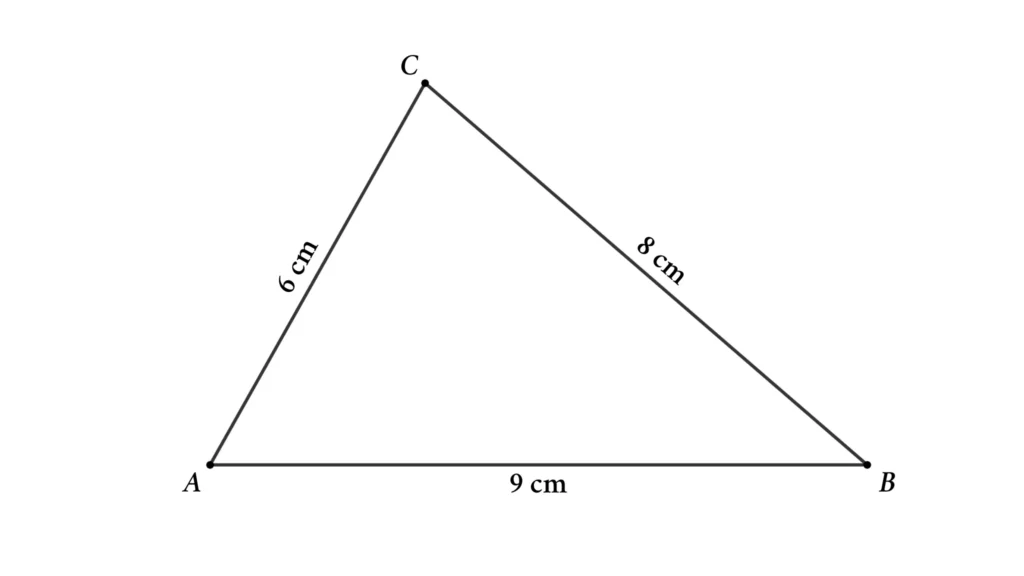
Solution: Radius of the circumcircle of the triangle
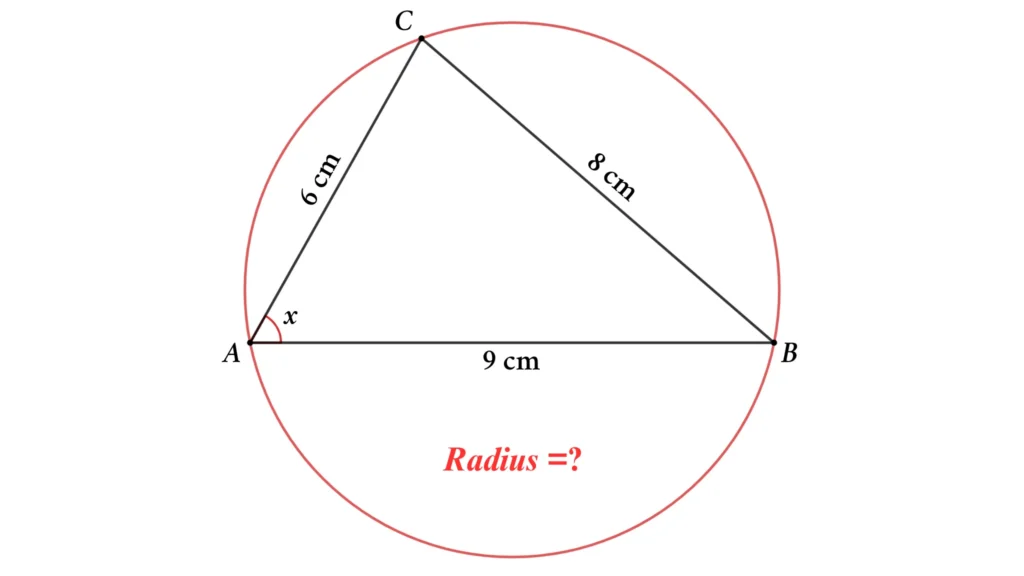
Let’s assume ∠BAC = x
Apply the Cosine rule in triangle ABC
BC² = AB² + AC² – 2 × AB × AC × cos ∠BAC
⇒ 8² = 9² + 6² – 2 × 9 × 6 × cos x
⇒ 64 = 81 + 36 – 108cos x
⇒ 64 = 81 + 36 – 108cos x
⇒ 53 = 108cos x
⇒ cos x = 53/108
sin² x + cos² = 1
⇒ sin² x + 53²/108² = 1
⇒ sin² x + 53²/108²
⇒ sin² x = 1 – 2809/11664 = 8855/11664
⇒ sin x = √8855/108
Now use the Sine rule
Diameter of Circumcircle = BC/sin x
Diameter of Circumcircle = 8/(√8855/108) = 864/√8855 cm
Radius of the Circumcircle = 8/(√8855/108) = 432/√8855 cm
Problem 2: Length of the Median
Trigonometry Math Problems with Triangles 2: Find the length of the median of the triangle
Triangle ABC’s sides are AB = 12 cm, BC = 10 cm, and AC = 8 cm. Then find the length of the median of the triangle ABC from A to side BC.
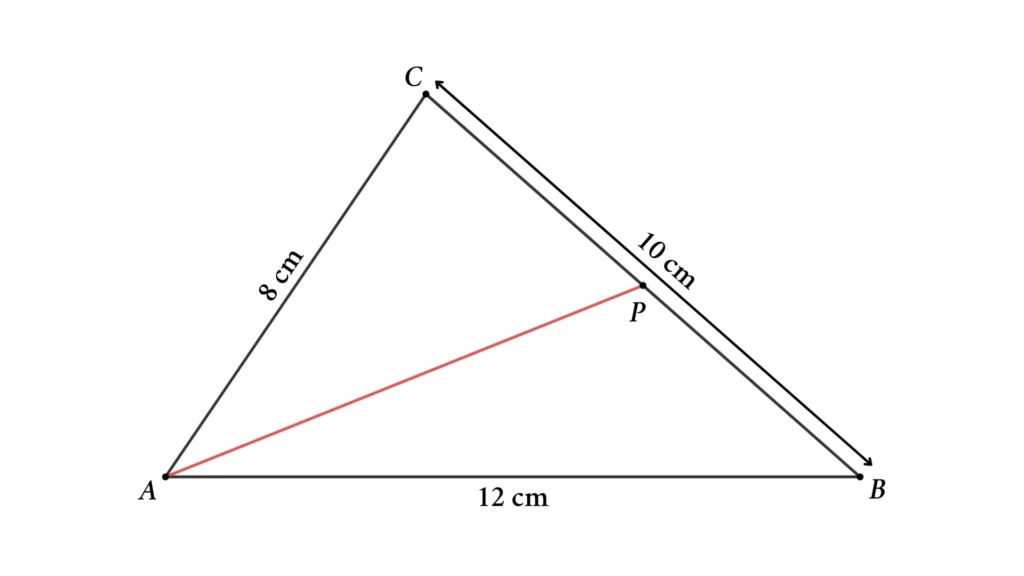
Solution: Length of the median.
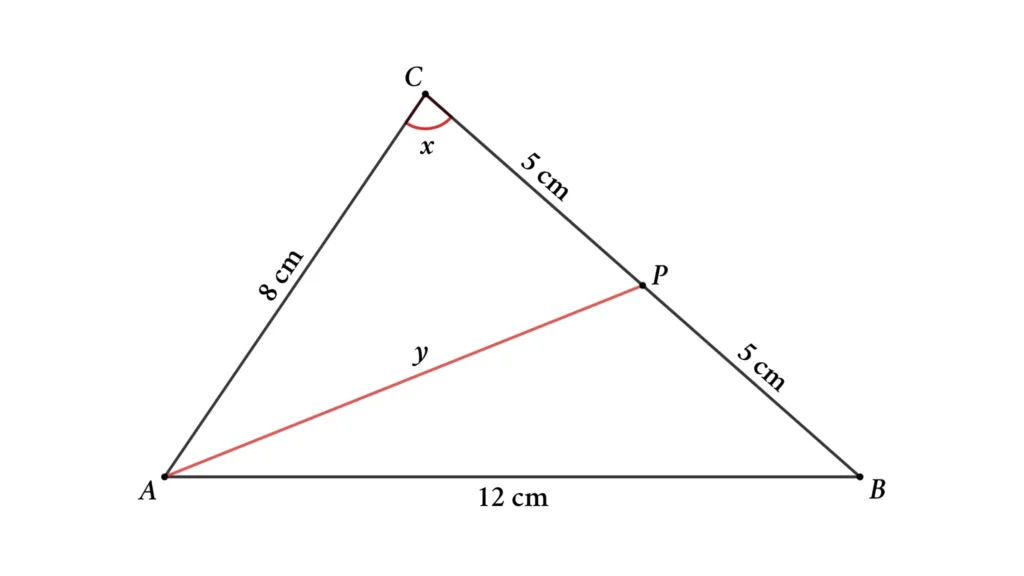
Let’s assume AP = y and ∠ACB = x
Apply the Cosine rule in triangle ABC
AB² = AC² + BC² – 2 × AC × BC × cos ∠ACB
⇒ 12² = 8² + 10² – 2 × 8 × 10 × cos x
⇒ 144 = 64 + 100 – 160cos x
⇒ 160cos x = 20
⇒ cos x = 1/8
Apply the Cosine rule in triangle APC
AP² = AC² + PC² – 2 × AC × PC × cos ∠ACB
⇒ y² = 8² + 5² – 2 × 8 × 5 × cos x
⇒ y² = 64 + 25 – 80 × 1/8
⇒ y² = 79
⇒ Length of the median = AP = y = √79 cm
Problem 3: Find the Height of the Triangle
Trigonometry Math Problems with Triangles 3: Find the Height of the Triangle
From triangle ABC, AB = 12 cm, ∠BAC = 30° and ∠ABC = 45°, Then find the height of the triangle
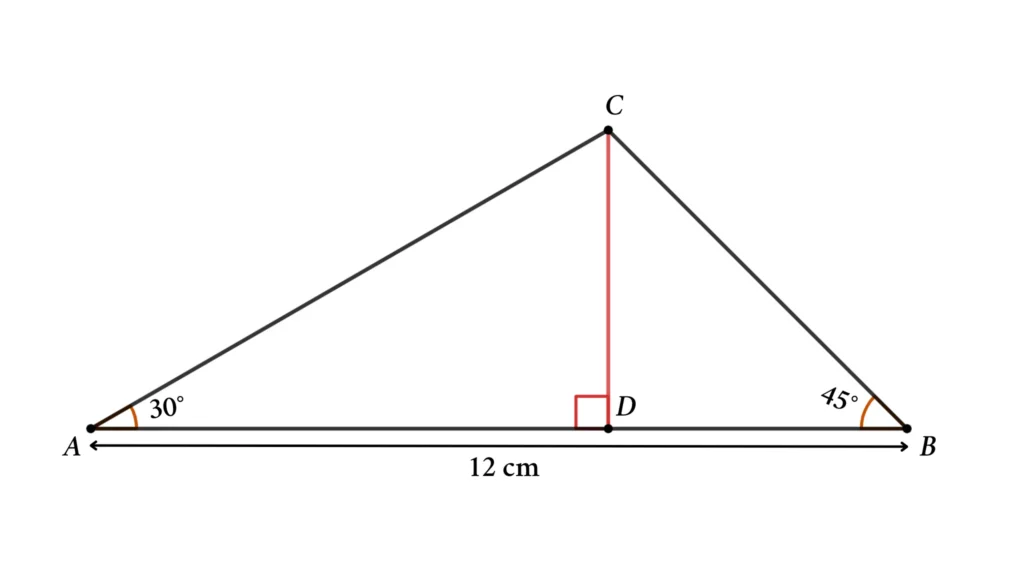
Solution: Height of the Triangle
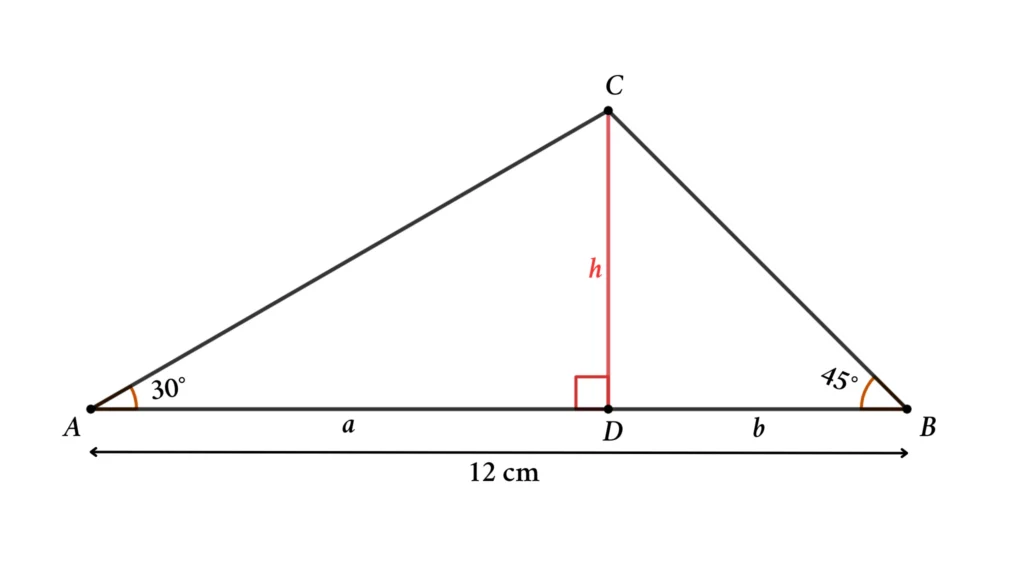
Let’s assume AD = a and BD = b
From figure,
tan ∠BAC = CD/AD
⇒ tan 30 = h/a
⇒ 1/√3 = h/a
⇒ a = h√3
tan ∠ABC = CD/BD
⇒ tan 45 = h/b
⇒ 1 = h/b
⇒ b = h
a + b = 12 = h√3 + h
⇒ h(√3 + 1) = 12
⇒ h = 12/(√3 + 1)
⇒ h = 6√3 – 6 cm
⇒ Height of the Triangle, h = 6√3 – 6 cm
Problem 4: Area of the Irregular Polygon
Trigonometry Math Problems with Triangles 4: Find the area of the Irregular Polygon formed by combining 4 equal squares.
An L-shaped Irregular polygon is inscribed inside the right-angle triangle ABC. The L-shaped Irregular polygon PQRST is formed by combining 4 equal squares. If AB = 13 cm and ∠ABC = 45°, then find the area of the L-shaped Irregular polygon.
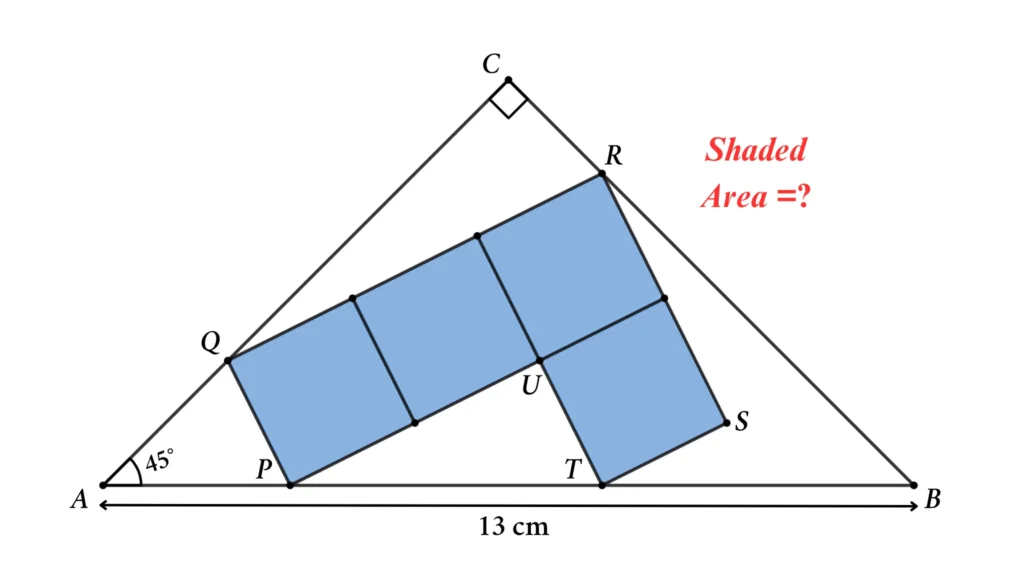
Solution: Area of the Irregular Polygon
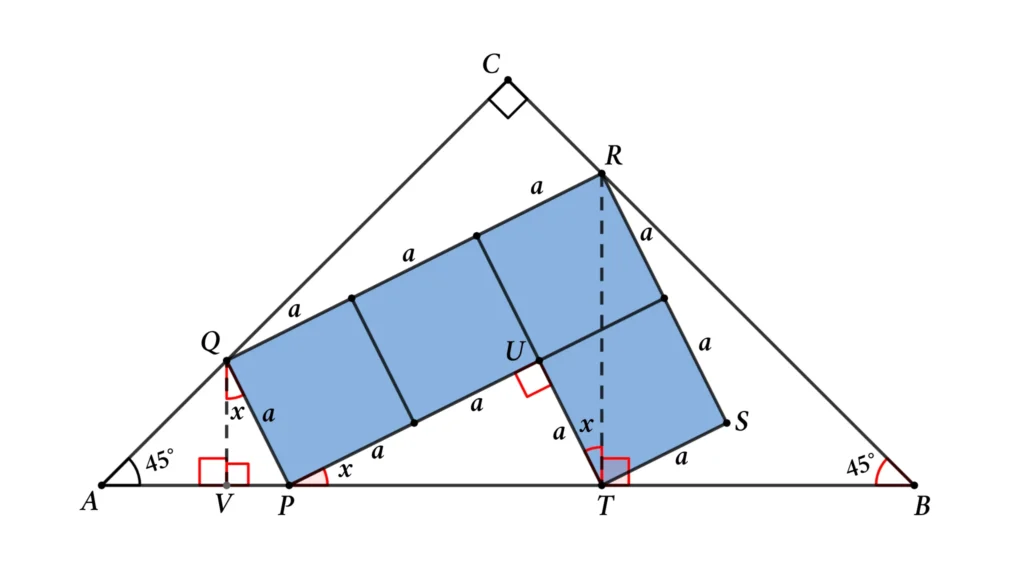
Let’s assume the sides of the square = a and ∠TPU = x
PQ = TU = TS = a (side of the square)
PU = 2a
RS = 2a
Apply Pythagoras theorem in triangle PTU
PT² = PU² + TU²
⇒ PT² = (2a)² + a²
⇒ PT² = 4a² + a² = 5a²
⇒ PT = a√5
Now
sin ∠TPU = TU/PT
⇒ sin x = a/a√5
⇒ sin x = 1/√5
cos ∠TPU = PU/PT
⇒ cos x = 2a/a√5
⇒ cos x = 2/√5
From triangle PQV
sin ∠PQV = PV/PQ
⇒ sin x = PV/a
⇒ 1/√5 = PV/a
⇒ PV = a/√5
cos ∠PQV = QV/PQ
⇒ cos x = QV/a
⇒ 2/√5 = QV/a
⇒ QV = 2a/√5
From triangle AVQ
tan ∠VAQ = VQ/AV
⇒ tan 45 = 2a/√5/AV
⇒ 1 = 2a/√5/AV
⇒ AV = 2a/√5
Apply Pythagoras theorem in triangle TSR
TR² = ST² + SR²
⇒ TR² = a² + (2a)² = a² + 4a² = 5a²
⇒ TR = a√5
From triangle TBR
tan ∠VAQ = TR/TB
⇒ tan 45 = a√5/TB
⇒ 1 = a√5/TB
⇒ TB = a√5
AB = AV + VP + PT + TB
⇒ AB = 2a/√5 + a/√5 + a√5 + a√5
⇒ 13 = 3a/√5 + 2a√5
⇒ 13√5 = 3a + 10a
⇒ 13√5 = 13a
⇒ a = √5
Area of L-shaped Irregular polygon PQRST = 4 × Area of the Square
⇒ Area of L-shaped Irregular polygon PQRST = 4 × a² = 4 × 5
⇒ Area of L-shaped Irregular polygon PQRST = 20 cm²
Problem 5: Area of the Triangle
Trigonometry Math Problems with Triangles 5: Find the area of the triangle
From the figure, triangle ABC is a right-angled triangle, ∠BAC = 30°, ∠BPC = 60° and AP = 5 cm then find the area of the triangle ABC.
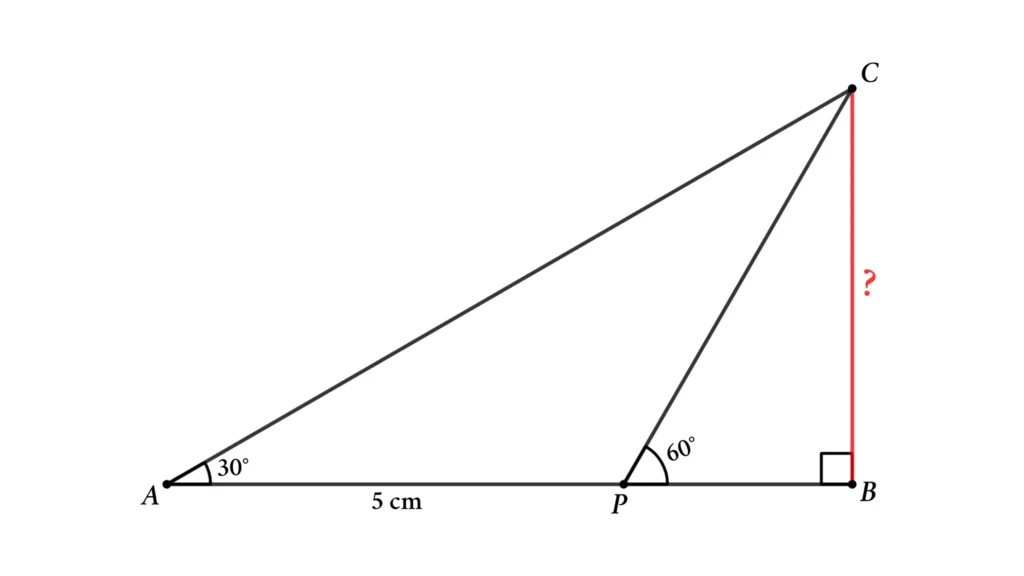
Solution: Area of the triangle
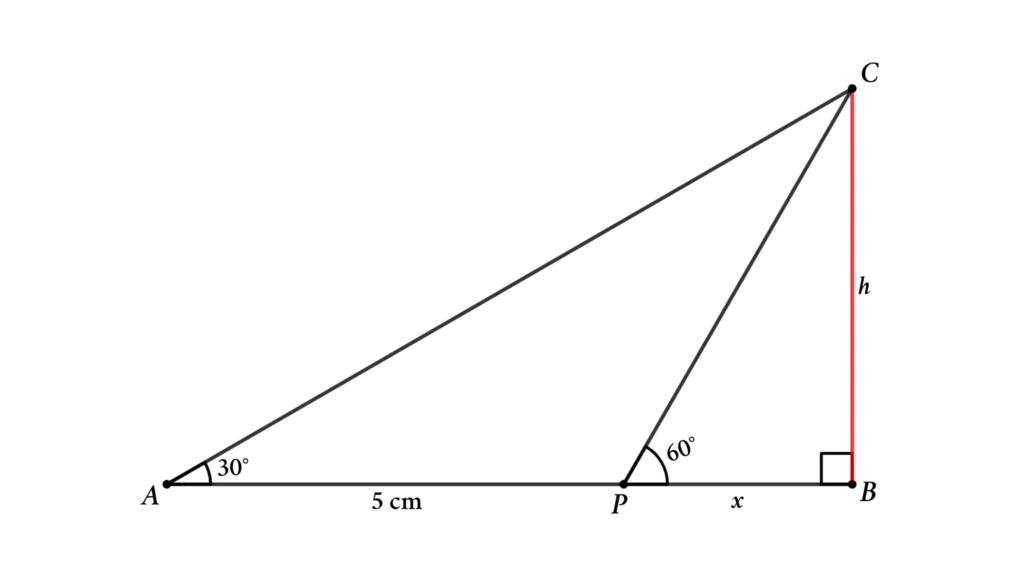
in figure
tan ∠BAC = BC/AB
⇒ tan 30° = h/(5 + x)
⇒ 1/√3 = h/(5 + x)
⇒ 5 + x = h√3
⇒ x = h√3 – 5
tan ∠BPC = BC/PB
⇒ tan 60° = h/x
⇒ √3 = h/x
⇒ x√3 = h
⇒ (h√3 – 5)√3 = h
⇒ 3h – 5√3 = h
⇒ 2h = 5√3
⇒ Height of the triangle ABC, h = (5√3)/2 cm
x = h√3 – 5 = ((5√3)/2)√3 – 5
x = 15/2 – 5
x = 5/2
area of the triangle = (AB × BC)/2
area of the triangle = ((5 + 5/2) × (5√3)/2)/2
area of the triangle = ((15/2) × (5√3)/2)/2
area of the triangle = (75√3)/8 cm²