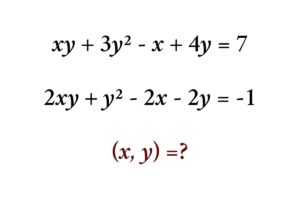System of Higher Degree Equations on Two Variables

Algebra Math Problem: How to solve the system of higher degree equations on two variables

Find the real roots of the system of higher degree equations, x⁴ + y⁴ = 82 and x – y = 2

Solution

Let

x⁴ + y⁴ = 82………..eq(1)

x – y = 2……………..eq(2)

assume x = u + v and y = u – v, then

From equation 2

x – y = u + v – (u – v)

⇒ 2 = u + v – u + v

⇒ 2 = 2v

so, v = 1

From equation 1

x⁴ + y⁴ = 82

⇒ 82 = (u + v)⁴ + (u – v)⁴

substitute v = 1

82 = (u + 1)⁴ + (u – 1)⁴

simplify the equation

82 = u⁴ + 4u³ + 6u² + 4u + 1 + (u⁴ – 4u³ + 6u² – 4u + 1)

⇒ 82 = 2u⁴ + 12u² + 2

⇒ 2u⁴ + 12u² – 80 = 0

thus, u⁴ + 6u² – 40 = 0

This is a quadratic equation with u², We can solve this equation with the use of factorization

u⁴ + 6u² – 40 = u⁴ + 10u² – 4u² – 40

⇒ 0 = u²(u² + 10) – 4(u² + 10)

⇒ 0 = (u² + 10)(u² – 4)

From the equation we get

u² + 10 = 0 or u² – 4 = 0

⇒ u² = 10 or u² = 4

that is, u = ±√-10 or u = ±√4

When u = ±√-10 x has no real roots

so, u = ±2

When u = 2, then

x = u + v = 2 + 1 = 3

y = u – v = 2 – 1 = 1

When u = – 2, then

x = u + v = – 2 + 1 = -1

y = u – v = – 2 – 1 = -3

then solution to the system of higher degree equations are (3, 1), ( – 1, – 3)