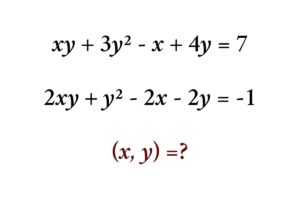Solve the quadratic equation √(x – 2) + √(4 – x) = √(6 – x) by factoring
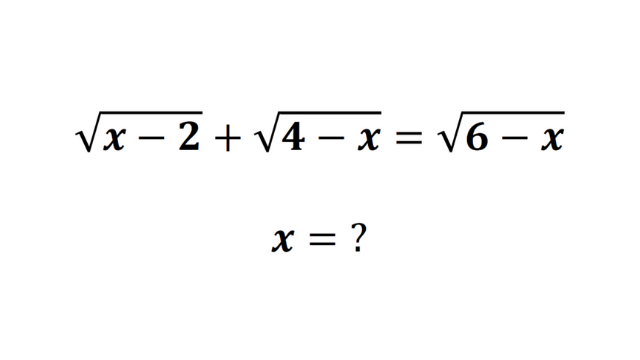
Solution
√(x – 2) + √(4 – x) = √(6 – x)
Square both sides then
(x – 2) + 2 × √(x – 2) × √(4 – x) + (4 – x) = 6 – x
We can rearrange this equation
2 + 2 × √(x – 2) × √(4 – x) = 6 – x
⇒ 2 × √(x – 2) × √(4 – x) = 4 – x
Again square both sides
2 × (x – 2) × (4 – x) = (4 – x)²
⇒ (4 – x)² – 4 × (x – 2) × (4 – x) = 0
We can solve this quadratic equation by factoring
⇒ (4 – x) (4 – x – 4(x – 2)) = 0
so, (4 – x) (4 – x – 4x + 8) = 0
Then, (4 – x)(-5x + 12) = 0
Now we got (4 – x) and (-5x + 12) is the factors of the quadratic equation
then
4 – x = 0 or -5x + 12 = 0
so x = 4, 12/5