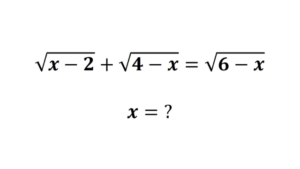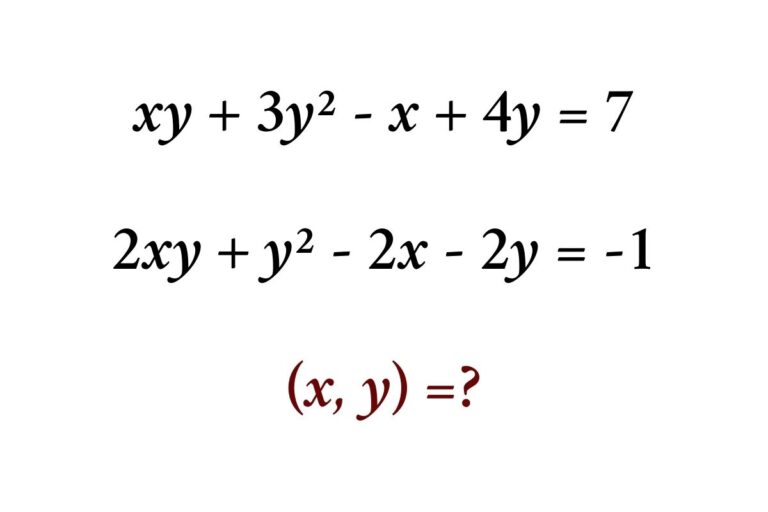
Solve the system of quadratic equations by elimination
If xy + 3y² – x + 4y = 7 and 2xy + y² – 2x – 2y = -1 then solve the system of quadratic equations using elimination
Solution
Equations have two variables, we need a single-variable quadratic equation to apply the quadratic formula or solve using factorization. We can do this by eliminating one variable from given equations, so we can create a new equation in a single variable
Let
xy + 3y² – x + 4y = 7…………..eq(1)
2xy + y² – 2x – 2y = -1………….eq(2)
Multiply equation 1 with 2
2(xy + 3y² – x + 4y) = 2 × 7
⇒ 2xy + 6y² – 2x + 8y = 14………eq(3)
subtract equation 2 from equation 3 then
2xy + 6y² – 2x + 8y – (2xy + y² – 2x – 2y) = 14 – (-1)
⇒ 2xy + 6y² – 2x + 8y – 2xy – y² + 2x + 2y = 14 + 1
⇒ 5y² + 10y = 15
We can simplify this equation to y² + 2y – 3 = 0, This is a simple quadratic equation in y so we can apply factorization to find the value of y
y² + 2y – 3 = y² – y + 3y – 3
⇒ y² + 2y – 3 = y(y – 1) + 3(y – 1)
⇒ y² + 2y – 3 = (y – 1)(y + 3)
so, (y – 1)(y + 3) = 0
Thus, y = 1 or y = -3
When y = 3 from equation 1
xy + 3y² – x + 4y = 7
⇒ -3x + 3(9) – x + 4(-3) = 7
⇒ -4x = -8
Thus, x = 2
When y = 1 from equation 1
xy + 3y² – x + 4y = 7
⇒ x + 3 – x + 4 = 7
⇒ x – x = 0
which means any real value of x satisfy y = 1 or x ∈ R
So solutions of (x, y) are (2, -3) and (1, R)