In this article, I represent geometry math problems for squares. This article is beneficial for students.
Problem 1: Area between the two Quarter-Circles.
Find the area between the two quarter-circles inscribed inside a square.
The figure shows a square and two quarter-circles. If the side length of the square is 4 cm, then find the area of the blue-shaded region
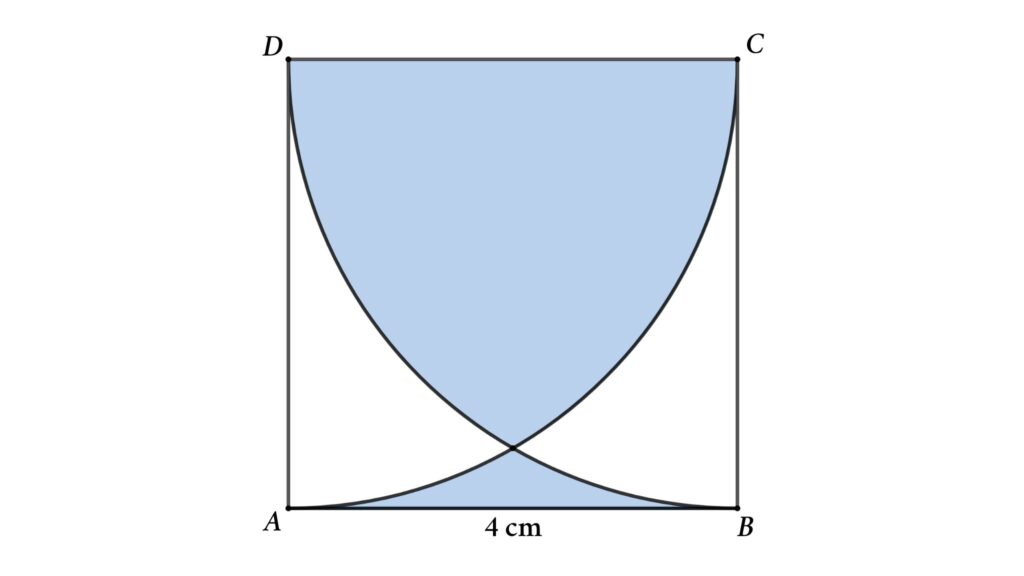
Solution: To solve this problem connect DQ, PQ, and CQ
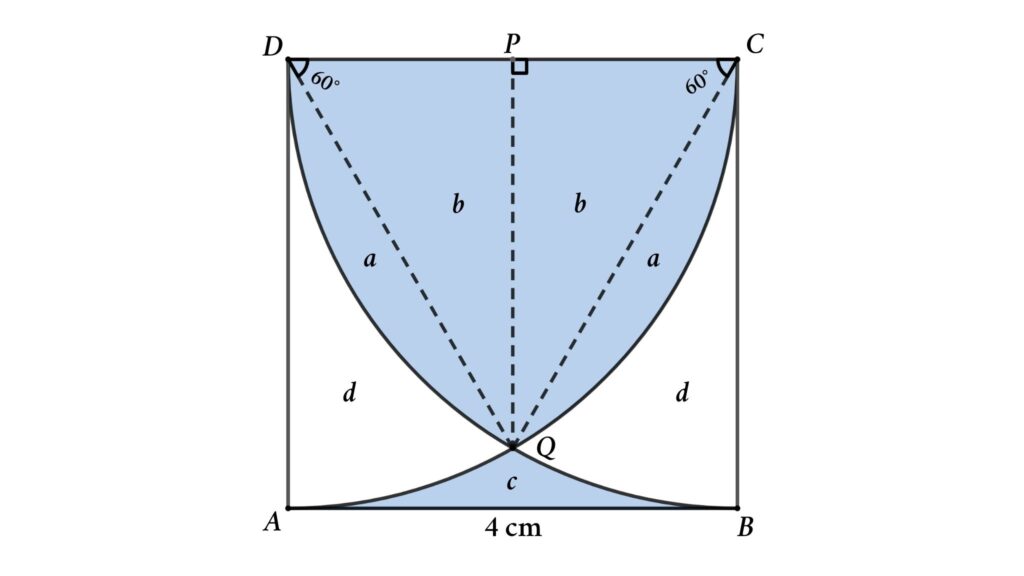
From figure,
CD = CQ = DQ = 4 cm
Area of sector DCQ = a + 2b = \({60 \over 360} \times \pi \times 4^2\) = \({8 \pi \over 3} \ \mathrm{cm^2}\)
⇒ a + 2b = \({8 \pi \over 3} \ \mathrm{cm^2}\) ……eq(1)
Area of △DCQ = 2b = \({1 \over 2} \times 4 \times 4 \times \sin 60 \) = \(4 \sqrt{3} \ \mathrm{cm^2}\)
⇒ 2b = \(4 \sqrt{3} \ \mathrm{cm^2}\) ……eq(2)
From eq(1) and eq(2) we get
a = \({8 \pi \over 3}\) – \(4 \sqrt{3}\) \(\mathrm{cm^2}\)
Area of quarter circle BCD = 2a + 2b + d = \({1 \over 4} \times \pi \times 4^2\) = \(4 \pi\) \(\mathrm{cm^2}\)
⇒ 2a + 2b + d = \(4 \pi\) \(\mathrm{cm^2}\) ……eq(3)
⇒ \({16 \pi \over 3}\) – \(8 \sqrt{3}\) + \(4 \sqrt{3}\) + d = \(4 \pi\)
⇒ d = \(4 \sqrt{3} \) – \({4 \pi \over 3}\) \(\mathrm{cm^2}\)
Blue shaded area = Area of the square – 2d = \(4^2\) – \(8 \sqrt{3} \) + \({8 \pi \over 3}\)
Blue shaded area = Area of the square – 2d = 16 – \(8 \sqrt{3} \) + \({8 \pi \over 3}\) \(\mathrm{cm^2}\)
Problem 2: Area of the Irregular Polygon.
Area of the geometry shape (Irregular Polygon) inside three squares.
The figure shows three squares with sides 6 cm, 8 cm, and 10 cm. Find the area of the blue-shaded region or find the area of the irregular polygon CDFHI.
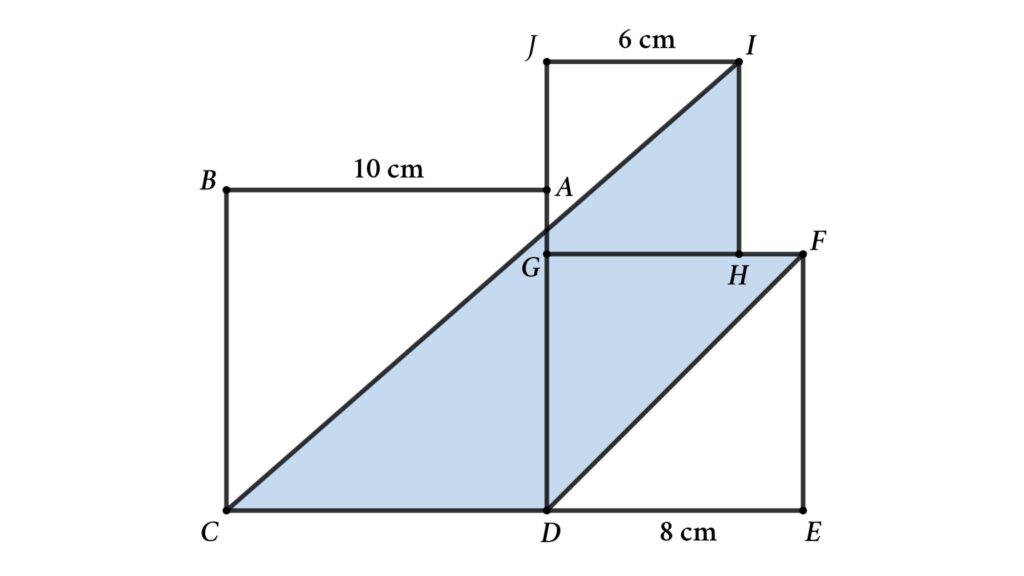
Solution: To solve this problem, extend IJ and CB then we will get a rectangle ABKJ
Here, shaded area = Area of region A + Area of region B + Area of region C
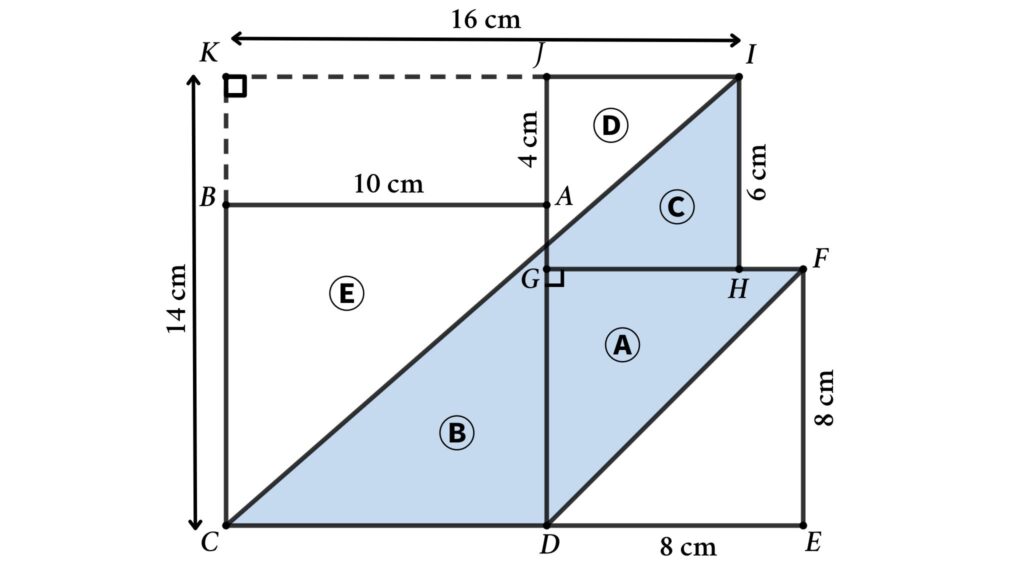
Area of region A = Area of △GDF = \({1 \over 2} \times GD \times DF \)
⇒ Area of region A = \({1 \over 2} \times 8 \times 8 \) = 32 \(\mathrm{cm^2}\)
Area of region B + Area of region C = Area of square ABCD + Area of square GHIJ – (Area of region D + Area of region E)
Area of region D + Area of region E = Area of △KCI – Area of rectangle ABKJ
Area of △KCI = \({1 \over 2} \times KC \times KI \) = \({1 \over 2} \times 14 \times 16 \)
⇒ Area of △KCI = 112 \(\mathrm{cm^2}\)
Area of rectangle ABKJ = \(KJ \times KB \) = \(10 \times 4 \)
⇒ Area of rectangle ABKJ = 40 \(\mathrm{cm^2}\)
⇒ Area of region D + Area of region E = 112 – 40 = 72 \(\mathrm{cm^2}\)
Area of square ABCD = \(AB^2 \) = \(10^2 \)
⇒ Area of square ABCD = 100 \(\mathrm{cm^2}\)
Area of square GHIJ = \(GH^2 \) = \(6^2 \)
⇒ Area of square GHIJ = 36 \(\mathrm{cm^2}\)
Area of region B + Area of region C = Area of square ABCD + Area of square GHIJ – (Area of region D + Area of region E)
⇒ Area of region B + Area of region C = 100 + 36 – 72 = 64 \(\mathrm{cm^2}\)
Shaded area = Area of region A + Area of region B + Area of region C = 32 + 64
⇒ Shaded area = 96 \(\mathrm{cm^2}\)
Problem 3: Area of the Quadrilateral
When the square is divided into four different quadrilaterals, calculate the quadrilateral’s area
From the figure, ABCD is a square, and P, Q, R, and S are midpoints Find the area of AQOP, If the area of BROQ = 39 cm², the area of CSOR = 27 cm², and the area of DPOS = 33 cm²

Solution: Connect AO, BO, CO, and DO then we will get 8 triangles
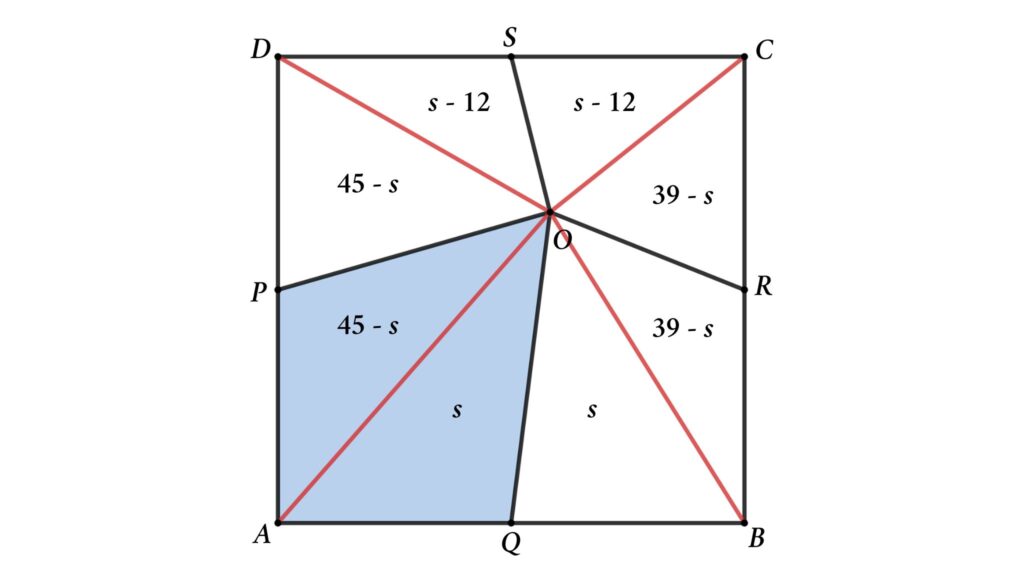
Assume the area of △AOQ = s
AQ = BQ so area of △BOQ = area of △AOQ = s
⇒ area of △BOR = area of BROQ – area of △BOQ = 39 – s
area of △COR = area of △BOR = 39 – s {BR = CR}
⇒ area of △COS = area of CSOR – area of △COR = 27 – (39 – s) = s – 12
area of △DOS = area of △COS = s – 12 {BR = CR}
⇒ area of △DOP = area of DPOS – area of △DOS = 33 – (s – 12) = 45 – s
Area of APOQ = area of △DOP + area of △AOQ = 45 – s + s = 45 cm²
Problem 4: Find the Area of the Square
From the figure find the area of the square ABCD
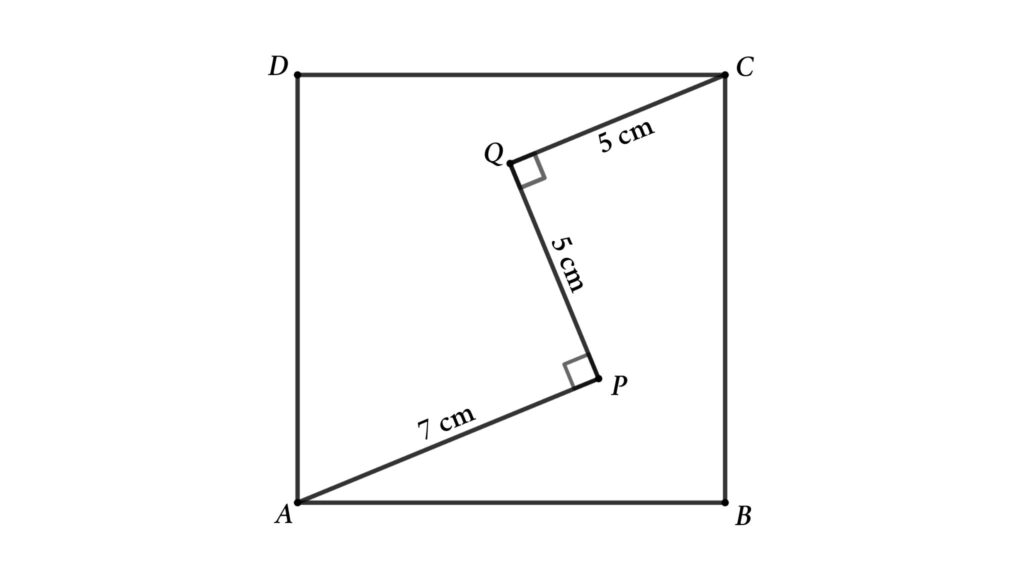
Solution: To solve the math problem, let’s start with extending AP and drawing a line parallel to PQ through C then we will get a triangle AKC

Where PQ = CK = 5 cm
PK = QC = 5 cm
⇒ AK = AP + PK = 7 + 5 = 12 cm
Apply Pythagoras’ theorem in △AKC
AC² = AK² + CK²
⇒ AC² = 12² + 5² = 144 + 25
⇒ AC² = 169
⇒ AC = 13 cm
Now apply Pythagoras’ theorem in △ADC
AC² = AD² + CD²
⇒ 169= 2 × AD² { AD = CD = sides of the square}
⇒ AD² = 169/2
Area of the square = AD² = 169/2 cm²
Problem 5: Square Made by Connecting the Midpoints
Find the area of the square made by connecting the midpoints of the sides and verticles
From the figure, ABCD is a square, and P, Q, R, and S are midpoints. then find the area of the smaller square inside the bigger square when the sides of the square are 4 cm.
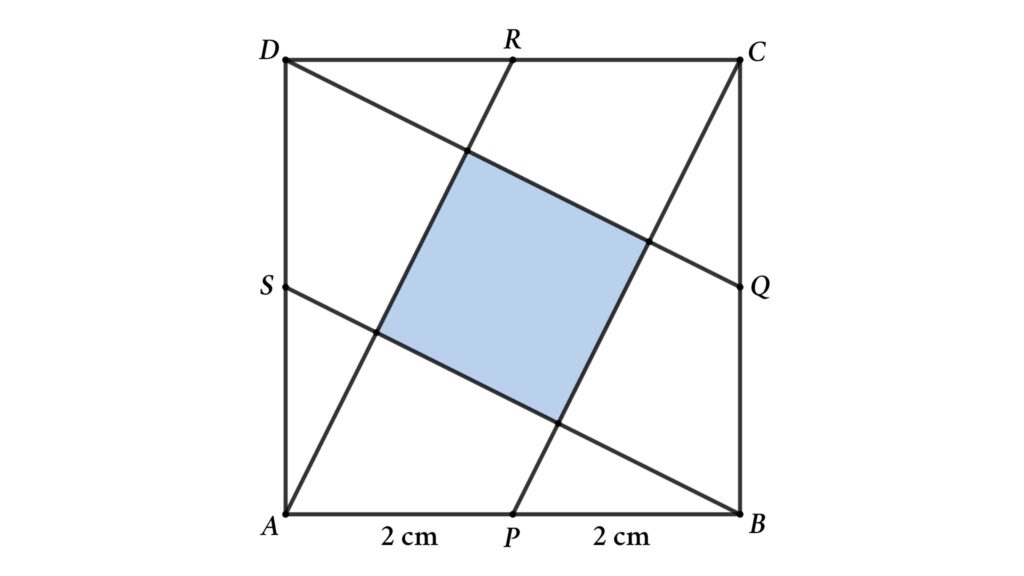
Solution
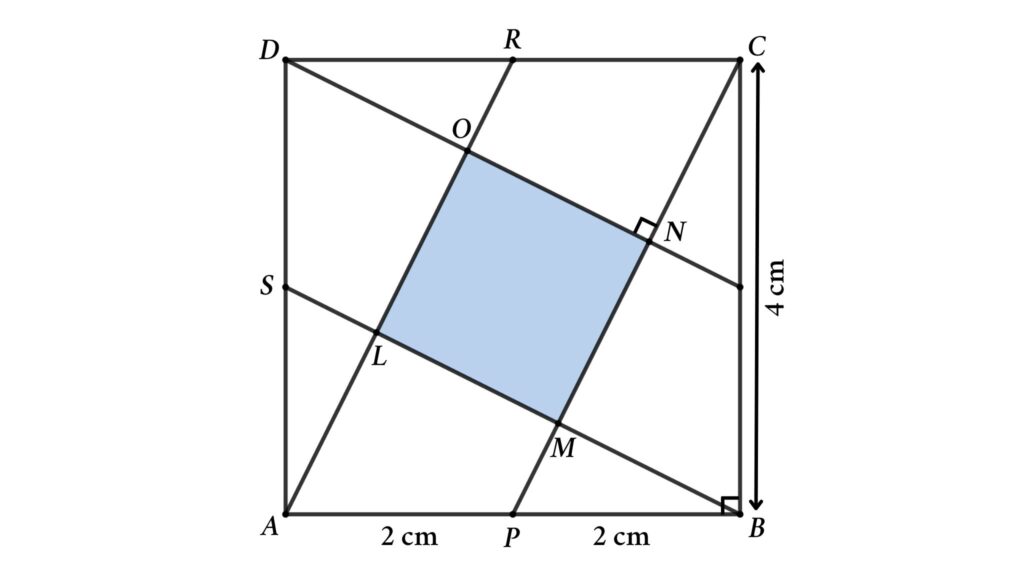
From the figure, the area of the square = LM²
Here we can find the area of the parallelogram APCR in two ways. that is,
Area of the parallelogram APCR = AP × CB = PC × LM (Where CB is the height of the parallelogram when AP is base, and LM is the height of the parallelogram when PC is base)
AP × CB = PC × LM
⇒ 2 × 4 = PC × LM
⇒ PC × LM = 8
⇒ LM = 8/PC
Now apply Pythagoras’ theorem in △PBC
PC² = PB² + CB²
⇒ PC² = 2² + 4² = 4 + 16
⇒ PC² = 20
⇒ PC = 2√5 cm
Then, LM = 8/PC = 8/(2√5)
⇒ LM = 4/√5
Area of the square = LM² = 16/5 cm²