10 Hard Geometry Math Problems for Circle

Chord and Tangents Geometry Math Problems

Problem 1: A semicircle inscribed inside a quarter circle. Find the length of a chord of the quarter circle that is also a tangent of the semicircle.

From the figure, a semicircle is inscribed inside a quarter circle, and PB is both the chord of the quarter circle and the tangent of the semicircle. Find the length of chord PB if the circle’s radius is 30 cm.

Solution: To solve the problem, we start by redrawing the figure as shown below.

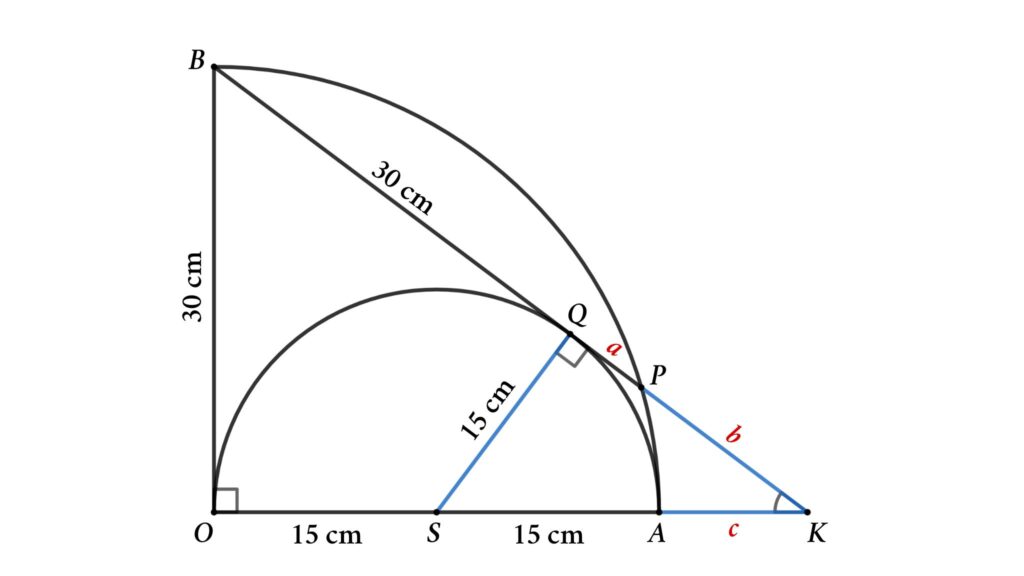
Here, SO = SA = SQ = 15 cm {radius of the semicircle}

OB = 30 cm (radius of the quarter circle)

BQ = OB = 30 cm (tangent from B)

Lets assume PQ = a, KP = b and AK = c

So, the length of the chord PB = BQ + QP = 30 + a

Consider △BOK and △QSK

Here △BOK and △QSK are similar triangles

Because

∠OKB = ∠SKQ (common for both triangles)

∠BOK = ∠SQK = 90°

so

OB/QS = OK/KQ = BK/KS

⇒ 30/15 = (30 + c)/(a + b) = (30 + a + b)/(15 + c)

⇒ 2 = (30 + c)/(a + b) = (30 + a + b)/(15 + c)

From, 2 = (30 + a + b)/(15 + c)

30 +2c = 30 + a + b

⇒ 2c = a + b

2 = (30 + c)/(a + b)

⇒ 2a + 2b = 30 + c

⇒ 4c = 30 + c

Then, 3c = 30

Or, c = 10 cm

⇒ a + b = 2c = 20 cm…………….eq(1)

In the next step, we turn the quarter circle into a circle (shown in the figure)

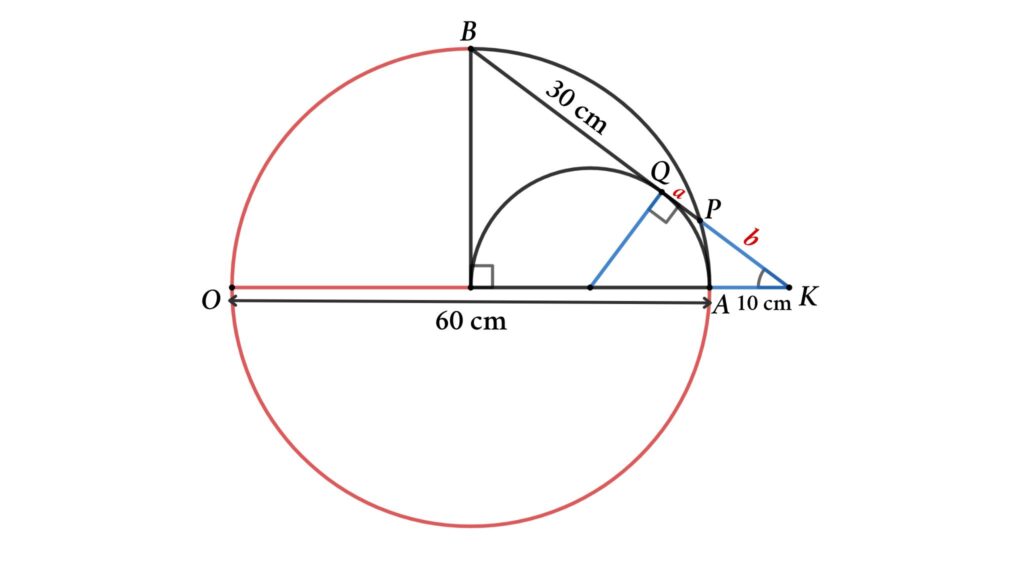
From figure

KA × KO = KP × KB (Intersecting secants theorem)

⇒ 10 × (10 + 60) = b × (30 + a + b)

⇒ 10 × (70) = b × (30 + 20) {a + b = 20}

So, 700 = 50b {a + b = 20}

⇒ b = 14 cm {a + b = 20}

a = 20 – 14 = 6 cm

Then, length of the chord PB = 30 + a = 30 + 6 = 36 cm

Problem 2: From the figure, two semicircles are met at Q. AM = 4 cm is the radius of the smaller semicircle, and BN = 8 cm is the radius of the bigger semicircle. MN is the tangent of both semicircles. PQ is perpendicular to tangent MN, then find the length of this perpendicular line

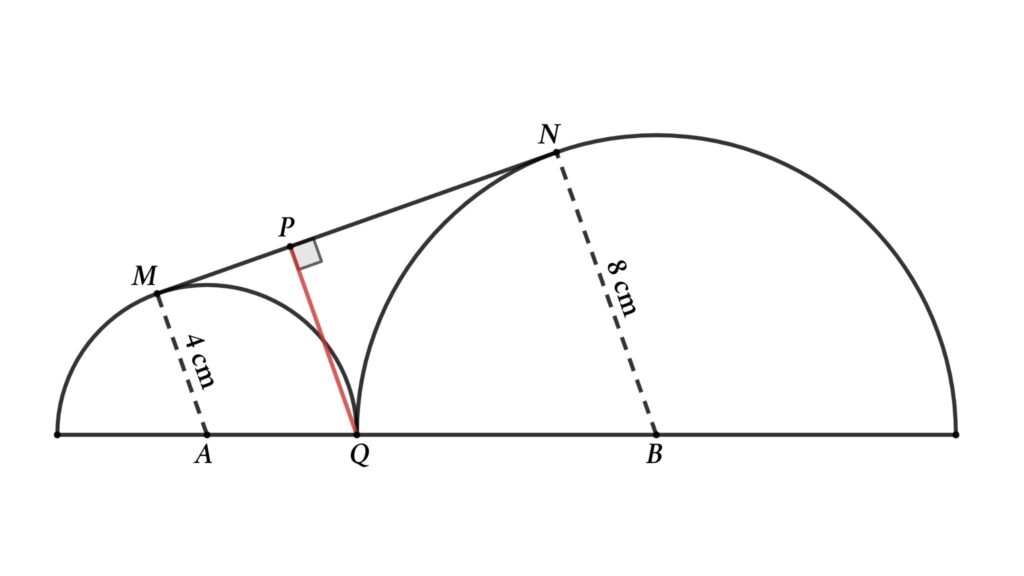
Solution: Let’s start by drawing a parallel line to AB. The line starts at M and ends at line BN.

Here, we get two triangles, △MPR and △MLN

From the figure

∠AMN = ∠MNB = 90° (MN is tangent of both semicircles)

AM = 4 cm (radius of the smaller semicircle)

AM = RQ = BL = 4 cm (AM, PQ & BL parallel lines and AB is parallel to ML)

Now consider △MPR and △MLN

△MPR and △MLN are similar triangles

Because

∠RMP = ∠MLN (common for both triangles)

∠MPR = ∠MNL = 90° (PQ and NM are parallel lines)

Then

PR/NL = MR/ML

⇒ PR/4 = 4/12

Or, PR/4 = 1/3

So, PR = 4/3 cm

⇒ PQ = RQ + PR = 4 + 4/3

⇒ PQ = 16/3 cm

That is, the length of the perpendicular line is 16/3 cm

Problem 3: Determine the area and perimeter of the circle when the length of two parallel chords and the distance between them are given.

From the figure, AB and CD are two parallel chords of the circle. Here AB = 20 cm and CD = 8 cm and the distance between the codes is 12 cm. Then find the area and perimeter of the circle.

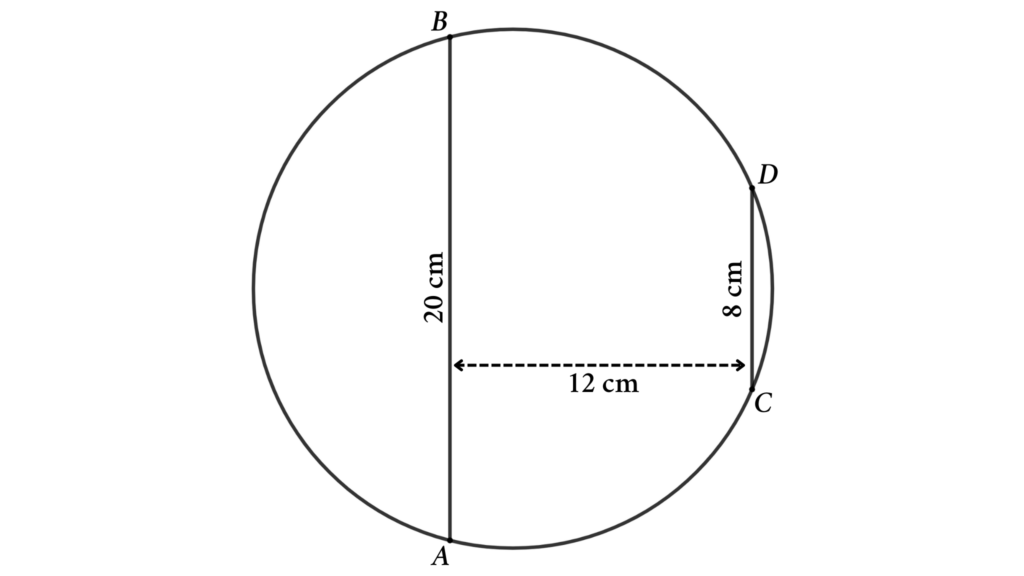
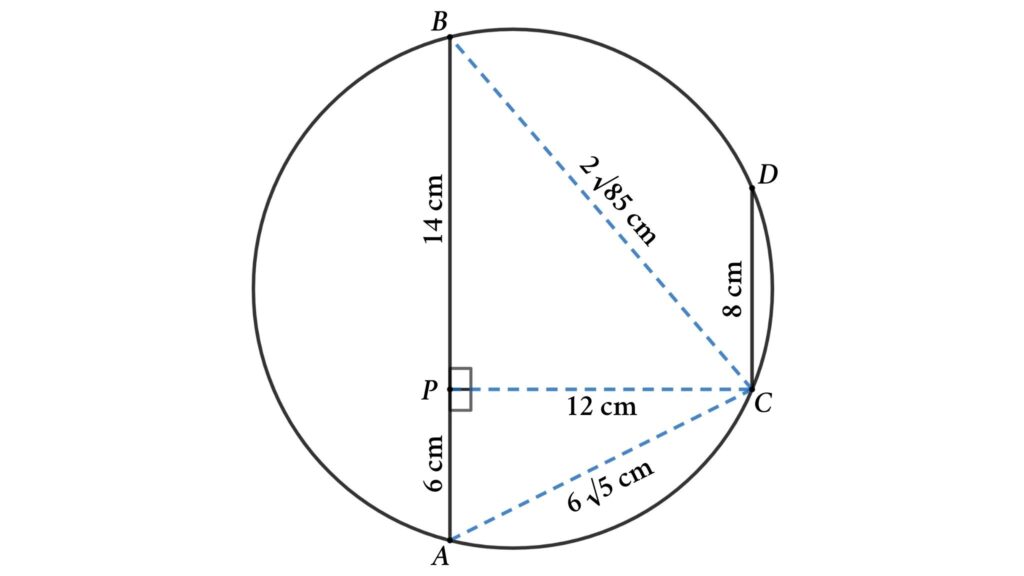
Solutions: Connect AC and BC and draw a perpendicular line PC from line AB to point C. Then we will get three triangles (△ABC, △PAC, and △PBC).

If the radius of the circumcircle is R, the area of the triangle is A, and the triangle’s sides are a, b, and c, then

$${A={{abc} \over 4R}}$$

Here PA = (AB – CD)/2 (due to symmetry)

⇒ PA = (20 – 8)/2 = 6 cm

Apply Pythagoras’ theorem in △PAC

AB² = PA² + PC²

⇒ AB² = 6² + 12² = 36 + 144 = 180

⇒ AB = √180 = 6√5 cm

Now apply Pythagoras’ theorem in △PBC

BC² = PC² + PB²

⇒ BC² = 12² + 14² = 144 + 196 = 340

⇒ AB = √340 = 2√85 cm

Here, area of △ABC = \(1 \over 2\) · AB · PC = \(1 \over 2\) · 20 · 12 = 120 cm²

\({A={{abc} \over 4R}}\)

⇒ \({120={{20 \times 6\sqrt{5} \times 2\sqrt{85}} \over 4R}}\)

⇒ R = \(\sqrt{425} \over 2\) = \({5\sqrt{17}} \over 2\) cm

Area of the circle = πR² = \(425 \pi \over 4\) cm²

Perimeter of the circle = 2πR = \(5\sqrt{17}\) cm

Problem 4: When the length of three chords from a point is given, find the circle’s radius.

From the figure, PA, PB, and PC are chords of the circle. here PA = 8√3 cm, PB = 18 cm and PC = 10√3 cm. If ∠BPA = ∠BPC then find the radius of the circle.

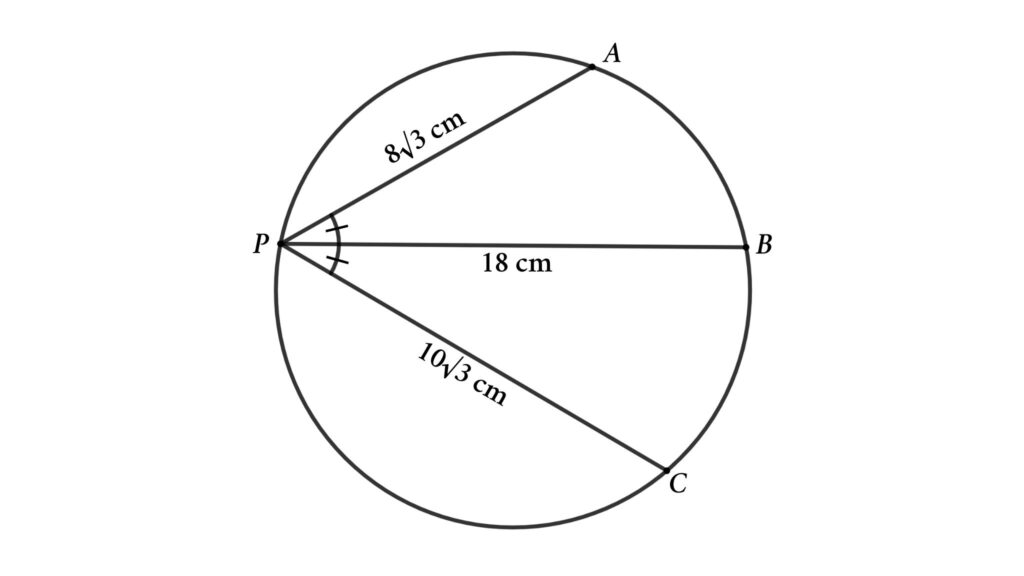
Solution: To solve the problem we start with connecting AB and CB. Here AB = CB because ∠BPA = ∠BPC and AB and CB are corresponding chords. Lets assume AB = CB = y and ∠BPA = ∠BPC = x

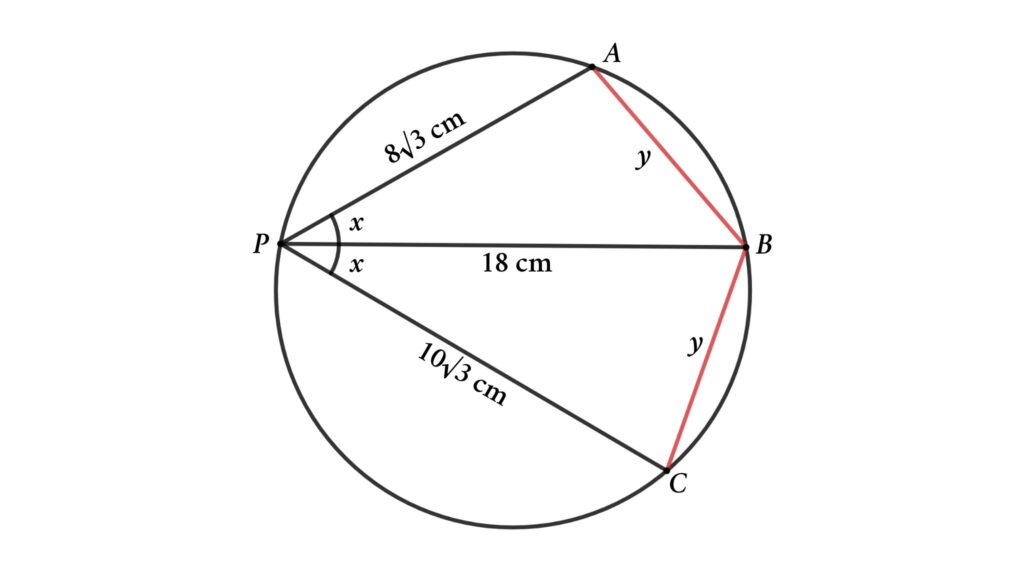
Here we have two triangles, we can apply the cosine rule for both triangles

From △PAB

AB² = PA² + PB² – 2 × PA × PB × cos ∠BPA

⇒ y² = (8√3)² + 18² – 2 × 8√3 × 18 × cos x

Thus, y² = 192 + 324 – 288√3 × cos x

⇒ y² = 516 – 288√3 × cos x ……………………………..eq(1)

From △PCB

CB² = PC² + PB² – 2 × PC × PB × cos ∠BPC

⇒ y² = (10√3)² + 18² – 2 × 10√3 × 18 × cos x

Thus, y² = 300 + 324 – 360√3 × cos x

⇒ y² = 624 – 360√3 × cos x ……………………………..eq(2)

From equation 1 and equation 2

516 – 288√3 × cos x = 624 – 360√3 × cos x

⇒ 72√3 × cos x = 108

⇒ cos x = (√3)/2 ……………………………………….eq(3)

Then

y² = 516 – 288√3 × cos x = 516 – 288√3 × (√3)/2

⇒ y² = 516 – 432 = 84

so, y = √84

y = 2√21 ………………………eq(4)

From equation 3

⇒ cos x = (√3)/2

x = 30°

so, sin x = 1/2

by using the sine rule we get y/sin x = 2R (∵ R is the radius of the circle)

y/sin x = 2R (∵ R is the radius of the circle)

⇒ (2√21)/(1/2) = 2R

⇒ R = 2√21 cm

So the radius of the circle is 2√21 cm

Triangle and Circle Math Problems

Problem 5: Determine the area of the smaller circle inside a right triangle. The circle touches a semi-circle inscribed inside the triangle, and two of the triangle’s sides are tangents to the circle.

△ABC is a right triangle, as shown in the figure. Where AB = 8 cm and AC = 6 cm. If BC and AC are tangents to the circle and semicircle, then find the area of the circle.

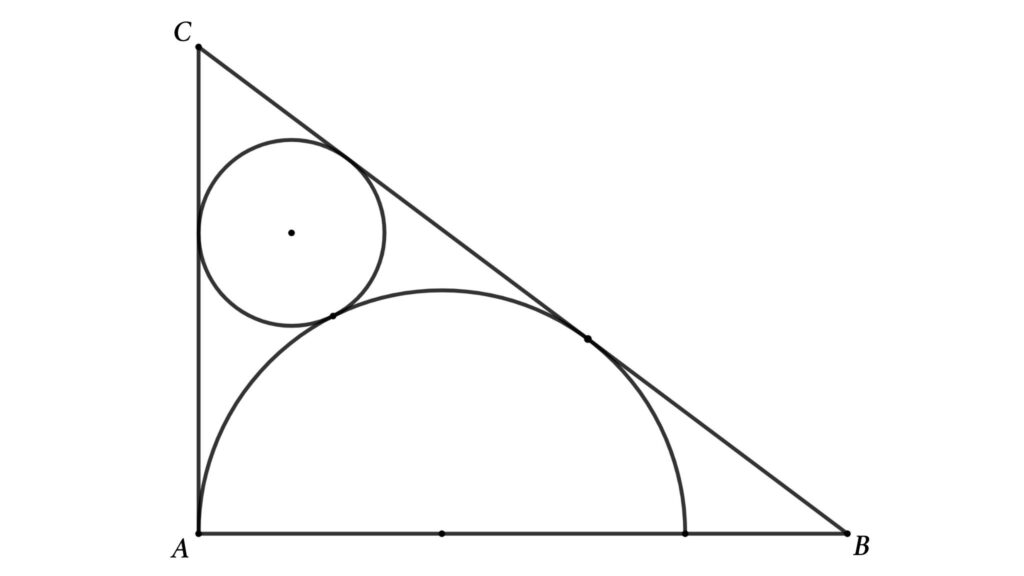
Solution: Assume the circle’s radius is r and the semicircle radius is R, and redraw the figure as shown below

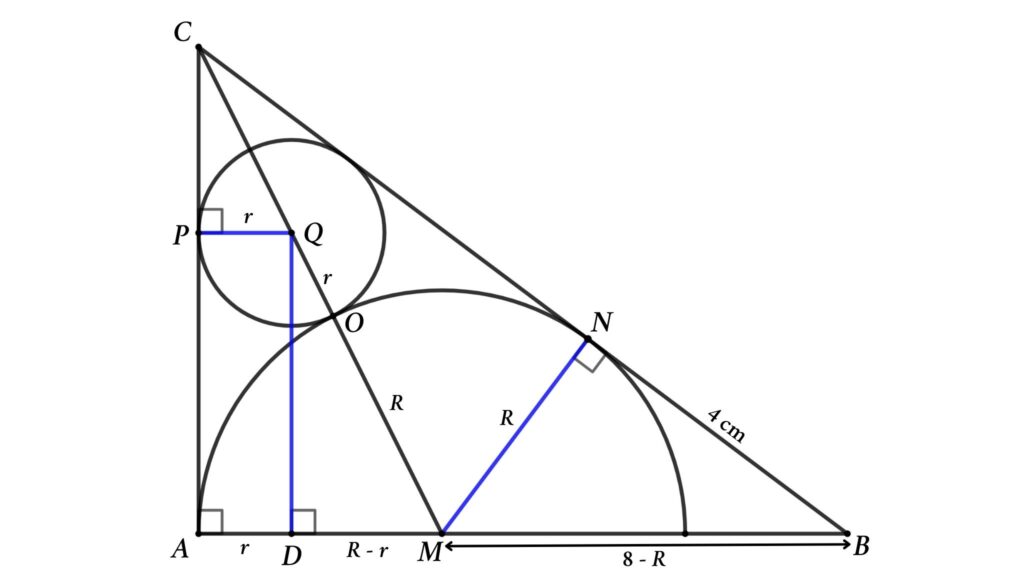
From the △ABC, using Pythagoras’ theorem we can find the length of BC

BC² = AB² + AC² = 8² + 6² = 64 + 36 = 100

BC = 10 cm

Here, AC = MN = 6 cm (tangent of the semicircle)

so, BN = 10 – 6 = 4 cm

Apply Pythagoras’ theorem in △MBN

BN² = BM² – MN²

⇒ 4² = (8 – R)² – R²

⇒ 16 = 64 – 16R + R² – R²

So, 16R = 48

Then, R = 3 cm

Now apply Pythagoras’ theorem in △DMQ

DQ² = MQ² – DM²

⇒ DQ² = (R + r)² – (R – r)²

⇒ DQ² = R² + 2Rr + r² – (R² – 2Rr + r²)

Thus, DQ² = 4Rr

So, DQ = AP = \(2\sqrt{Rr}\)

Here we get PC = 6 – \(2\sqrt{Rr}\)

Now consider △AMC and △QPC. Here PQ and AM are parallel lines so △AMC and △QPC are similar triangles, Then

PQ/AM = PC/AC

⇒ r/R = (6 – 2 √(Rr))/6

⇒ r/3 = (6 – 2 √(3r))/6

Then, r = 3 – √(3r)

⇒ √(3r) = 3 – r

⇒ 3r = (3 – r)²

Or, 3r = 9 – 6r + r²

Then, r² – 9r + 9 = 0

This is a quadratic equation, so

$$
\begin{align}
r &= {9 \pm \sqrt{9^2-4 \times 9 \times 1} \over 2} \
\end{align}
$$

$$
\begin{align}
r &= {9 \pm 3\sqrt{5} \over 2} \
\end{align}
$$

Here r is less than 9, then

$$
\begin{align}
r &= {9-3\sqrt{5} \over 2} \ \mathrm{cm}\
\end{align}
$$

Then the area of the circle is \(\pi \bigg({9-3\sqrt{5} \over 2} \bigg)^2 \) or \({63 \pi-27 \pi \sqrt{5} \over 2} \ \mathrm{cm^2} \)

Problem 6: When the sides of a triangle are given, find the area of the circumcircle.

In △ABC, AB = 8 cm, AC = 6 cm and BC = 4 cm. Then find the area of the circumcircle

Solution: If the radius of the circumcircle is R, the area of the triangle is A, and the triangle’s sides are a, b, and c, then

$${A={{abc} \over 4R}}$$

Now we can find the area of the triangle using Heron’s formula \({A=\sqrt{s(s-a)(s-b)(s-c)}}\)

Where s = (a + b + c)/2

s = (8 + 6 + 4)/2 = 18/2 = 9

Now

\({A=\sqrt{9(9-8)(9-6)(9-4)}}\) = \({\sqrt{9 · 1 · 3 · 5}}\) = 3√15 cm²

then

3√15 = (8 · 6 · 4)/(4R)

R = 16/√15 cm

Then the area of the circumcircle is \(\pi \bigg({16 \over \sqrt{15}} \bigg)^2 \) or \({256 \pi \over 15} \ \mathrm{cm^2}\)

Square and Circle Math Problems

Problem 7: Two squares are inscribed inside a quarter circle. Using the first square’s side length, determine the second square’s side length.

Two squares are inscribed inside a quarter circle. The larger square has a 2 cm side length. Calculate the side length of the smaller square

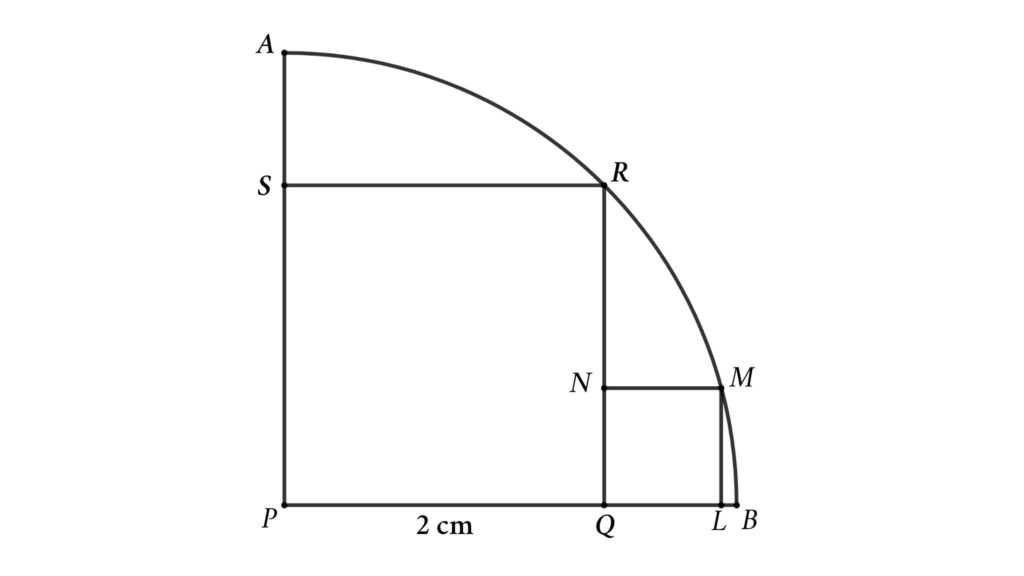
Solution: To solve the problem, let’s start with completing the quarter circle into a circle and extend RQ and MN. Assume the side length of the smaller square is x.

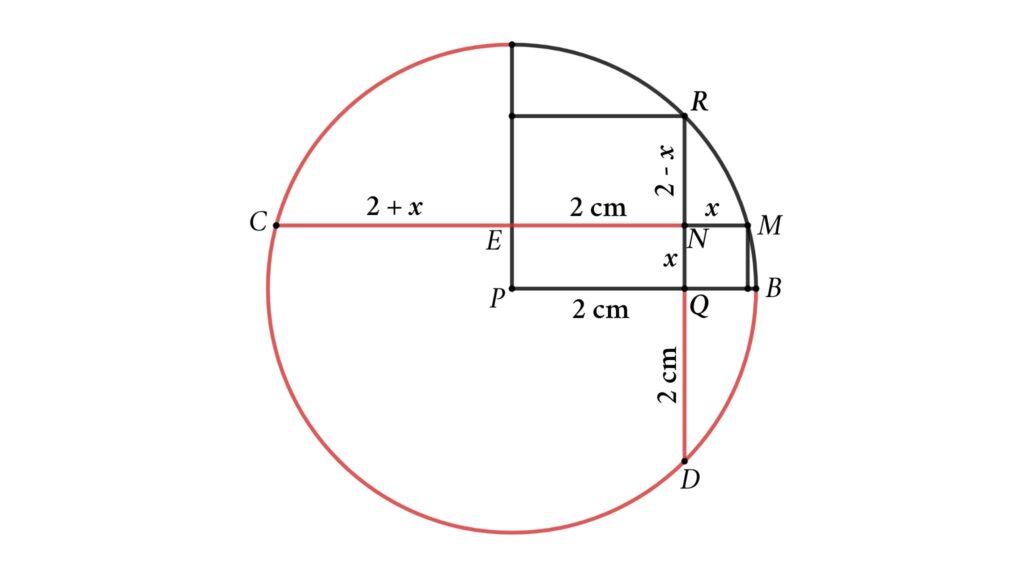
From the figure, we can see that chord CM and RD cross at N, so we get

CN × MN = RN × DN

Here

EN = PQ = 2 cm

EM = EC = 2 + x (due to symmetry)

⇒ CN = CE + EN = 2 + x + 2 = 4 + x

QR = QD = 2 cm

RN = RQ – NQ = 2 – x

DN = DQ + QN = 2 + x

Now we get

CN × MN = RN × DN (chord intersection theorem)

⇒ (4 + x) × x = (2 – x) × (2 + x)

⇒ 4x + x² = 4 – x²

Then, 2x² + 4x – 4 = 0

Or, x² + 2x – 2 = 0

This is a quadratic equation, so

$$
\begin{align}
x &= {-2 \pm \sqrt{(-2)^2-4 \times 1 \times (-2)} \over 2} \
\end{align}
$$

$$
\begin{align}
x &= {-1 \pm \sqrt{4+8} \over 2} \
\end{align}
$$

$$
\begin{align}
x &= {-1 \pm \sqrt{3}}
\end{align}
$$

Where \( x>0 \) so, \(x = {\sqrt{3}-1} \ \mathrm{cm} \)

Or side length of the smaller square = \( {\sqrt{3}-1} \ \mathrm{cm}\)

Problem 8: Determine the tangent length between the two quarter-circles enclosed by a square.

A square and two quarter-circles are in the figure. PQ is the tangent of both quarter circles. Find the length of PQ (length of tangent)

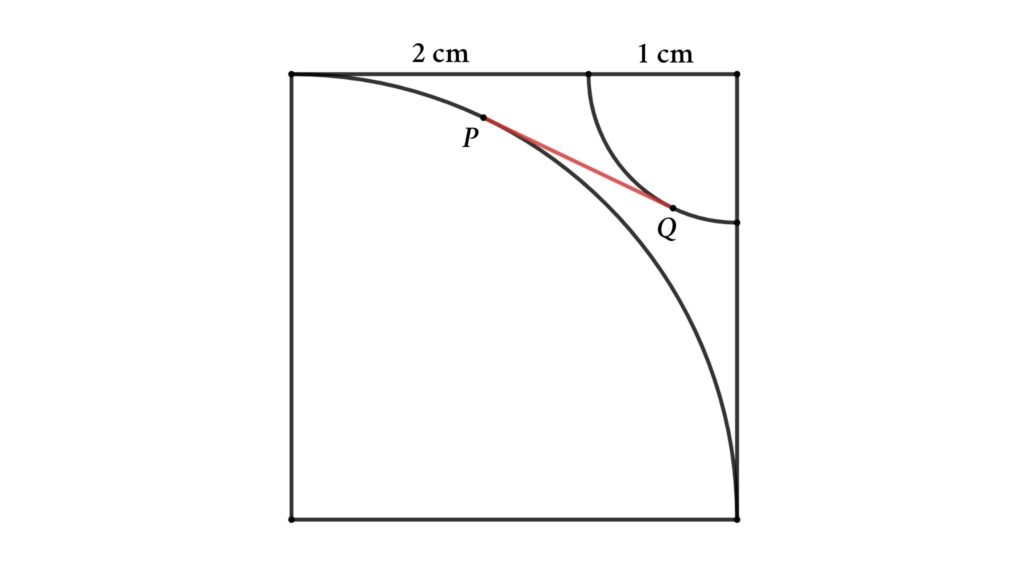
Solution: Create a right triangle shown in the figure (△ABC). Let’s assume the length of the tangent is x (PQ = x)

From figure

PQ || CB and PQ = CB = x

PC || BQ and PC = BQ = 1 cm

AP = 3 cm

AB = 3√2 cm

Now apply Pythagoras’ theorem in △ABC

AB² = AC² + BC²

⇒ (3√2)² = (AP + PC)² + x²

Or, (3√2)² = (3 + 1)² + x²

⇒ 18 = 16 + x²

⇒ x = √2 cm

That is the length of the tangent is √2 cm

Problem 9: A semicircle and circle inscribed inside a square. Find the radius of the circle.

A circle and semicircle are inscribed inside a square as shown in the figure

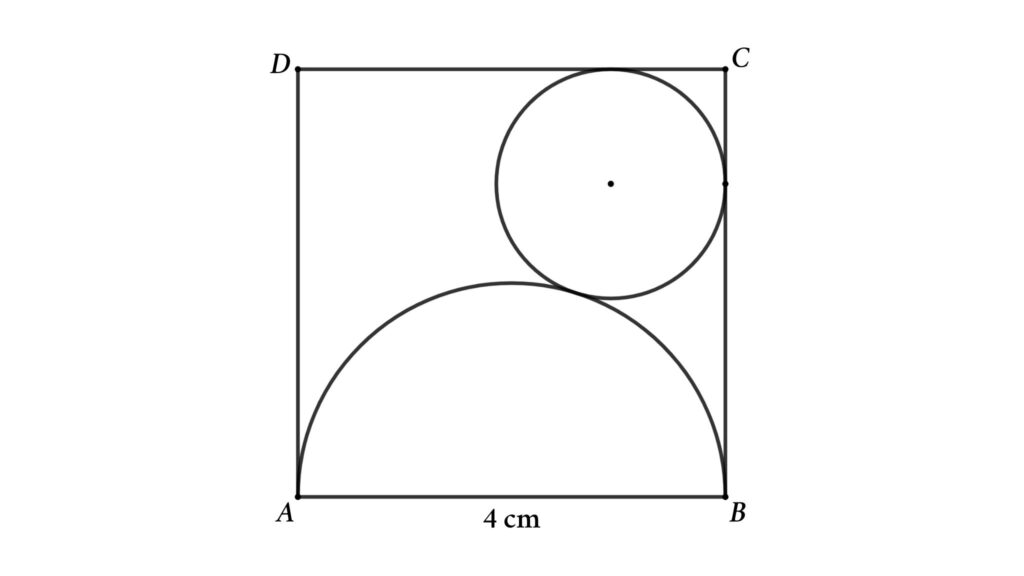
Find the radius of the circle if the side of the square is 4 cm.

Solution: Assume the radius of the circle is r and connect the center of the circle and semicircle to make a right triangle shown in the figure.

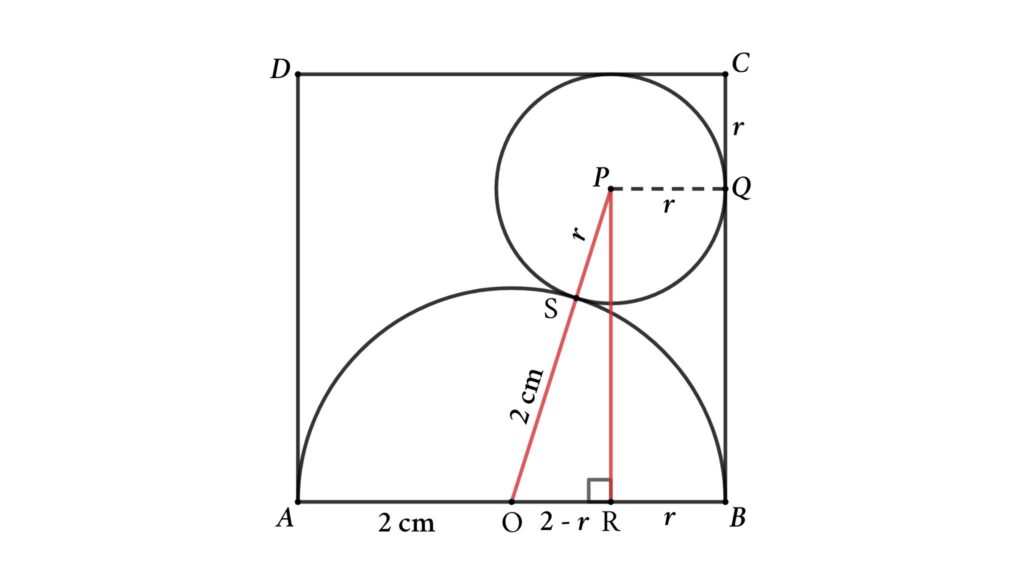
From figure

PQ = BR = PS = r (radius of the circle)

OA = OB = OS = 2 cm (radius of the semicircle)

OR = OB – BR = 2 – r

OP = OS + SP = 2 + r

Apply Pythagoras’ theorem in △OPR

PR² = OP² – OR²

⇒ PR² = (2 + r)² – (2 – r)²

⇒ PR² = 4 + 4r + r² – (4 – 4r + r²)

Thus, PR² = 8r

⇒ PR = √(8r)

⇒ BQ = √(8r)

Here, BC = BQ + QC = √(8r) + r = 4

⇒ 8r = (4 – r)²

⇒ 8r = 16 – 8r + r²

Or, r² – 16r + 16 = 0

This is a quadratic equation, so

$$
\begin{align}
r &= {-(-16) \pm \sqrt{(-16)^2-4 · 1 · 16} \over 2}\
\end{align}
$$

$$
\begin{align}
r &= {16 \pm 8 \sqrt{3} \over 2} = {8 \pm 4\sqrt{3}}\
\end{align}
$$

Here radius of the circle is less than 4 so \(r = {8 – 4\sqrt{3}} \) cm

Problem 10: A circle is inside a quarter-circle. Find the difference between areas.

A quarter circle with a radius of 6 cm is shown in the figure. A circle is drawn inside the quarter circle by touching the arc and one of its sides. Then find the area of the blue region.

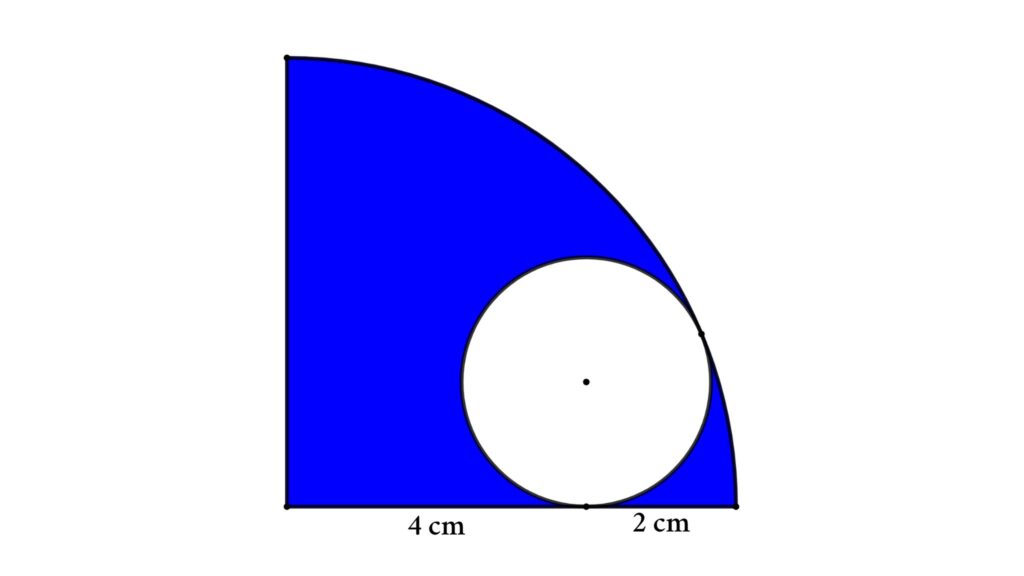
Solution: Assume the circle’s radius is r, and redraw the figure as shown below

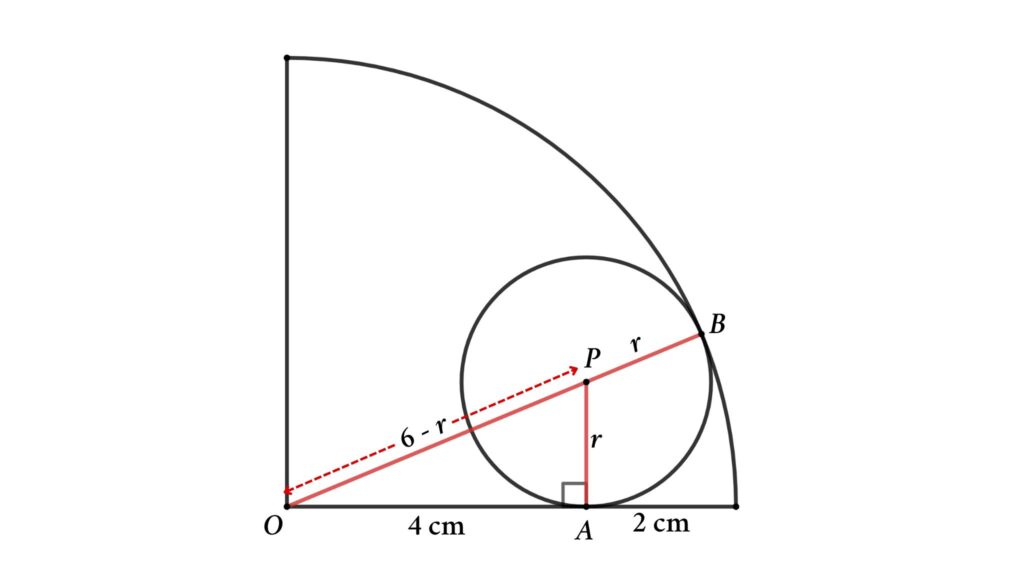
Here OB is the radius of the quarter circle so OB = 6 cm

OP = OB – PB = 6 – r

Now apply Pythagoras’ theorem in △OAP

OP² = OA² + AP²

⇒ (6 – r)² = 4² + r²

⇒ 36 – 12r + r² = 16 + r²

So, 12r = 20

⇒ r = 20/12 = 5/3 cm

That is the radius of the circle is 5/3 cm