Circular Sector and Segments
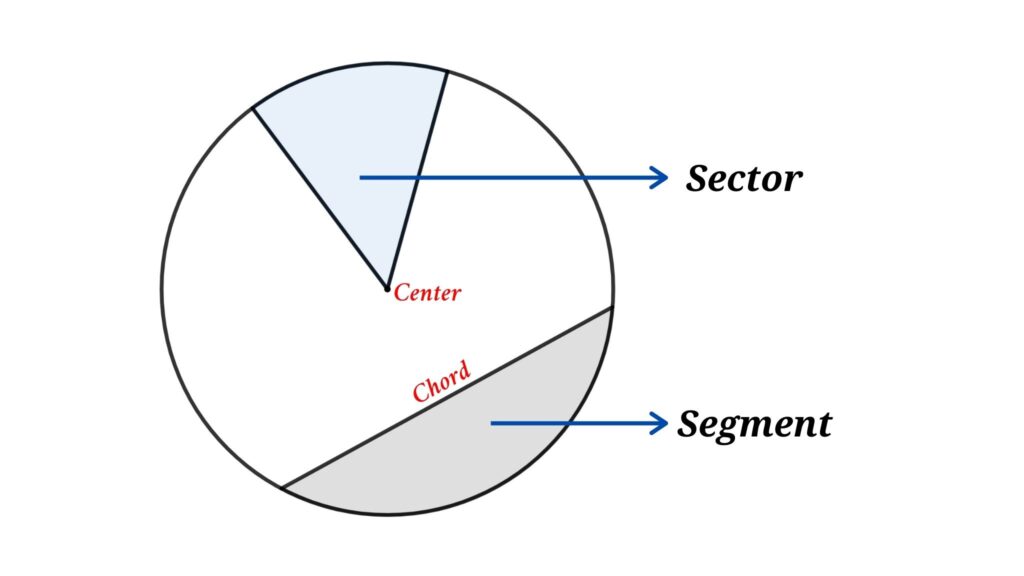
A sector of a circle is the region bounded by two radii and the corresponding arc, whereas a segment is a region bounded by a chord and the corresponding arc.
The sector of a circle
A circle is a standard shape in geometrical figures. A circle is associated with numerous concepts and formulas. A circular sector, also known as a circle sector, is a portion of a circle bounded by two radii and an arc.
Formation of the circular sector
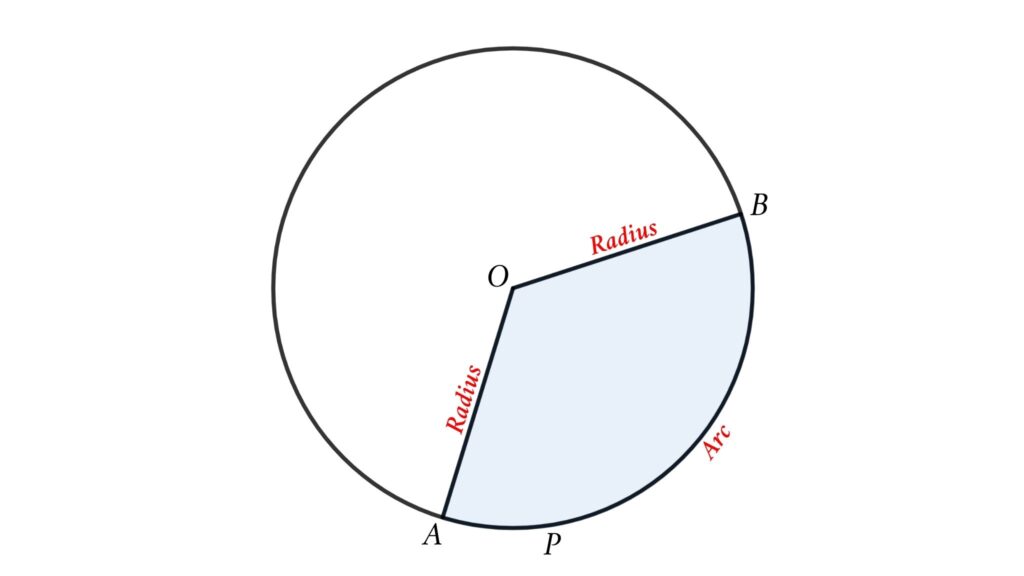
A circle sector is formed by cutting a circle through two radii, and a circular segment is formed by cutting a circle through its chords. A circular sector contains two radii and an arc. From figure OA = OB = Radius of the circle And APB is an arc
Major sector and minor sector of a circle
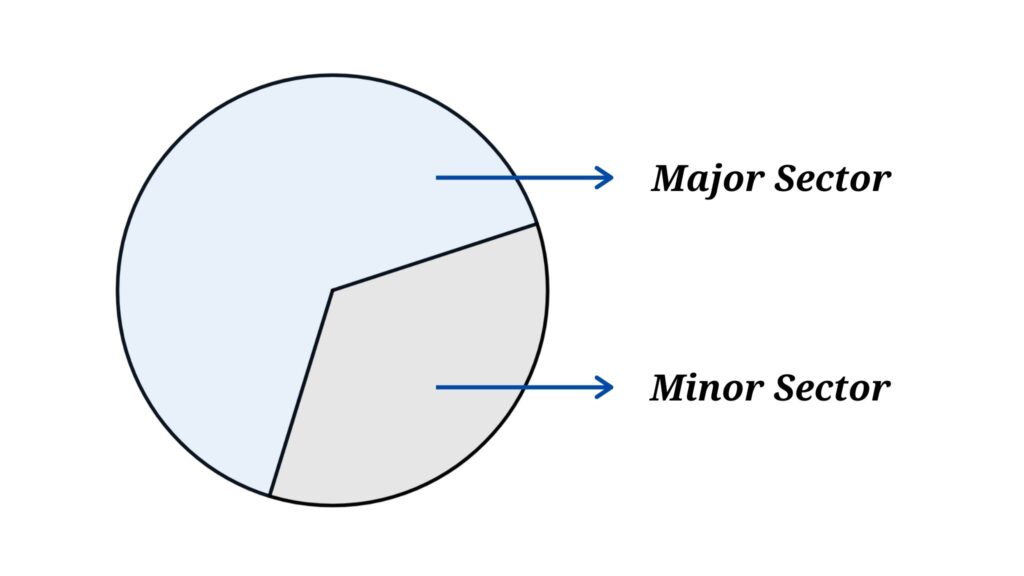
We saw how the circular sectors are forming. When we cut a circle then we have got at least two sectors. One of the circular sectors has a larger area than another sector, except all two sectors are a semicircles
Where the smaller area is known as the minor sector and the larger area is the major sector
Area and perimeter of a sector of a circle
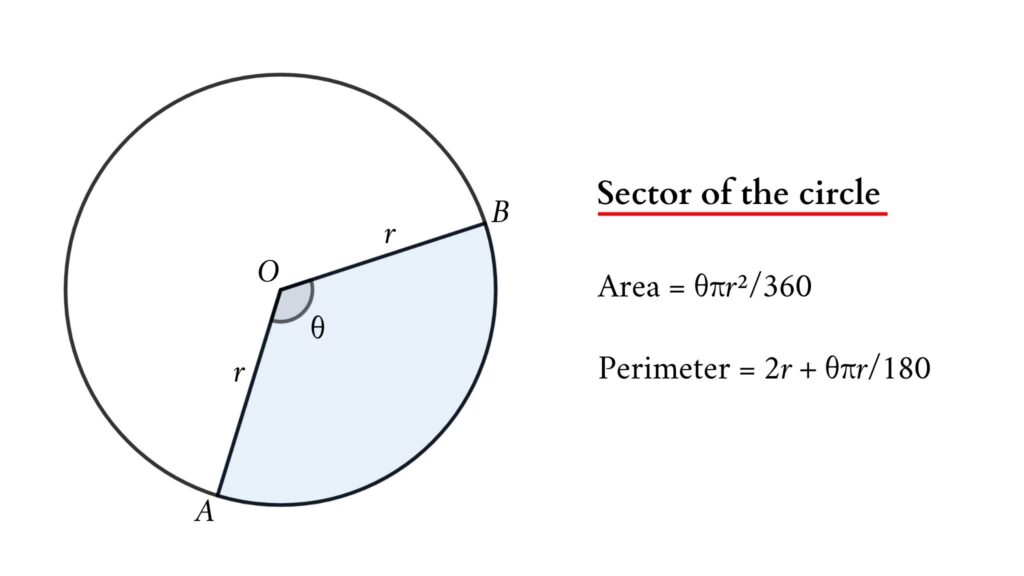
Area of a circular sector
We know the central angle of a circle is 360°. Let θ is the central angle of the sector
Then Area of circular sector = (θ/360) × Area of the circle
We know the area of a circle is πr²
so, Area of sector = (θ/360)×πr² = θπr²/360 (here θ is in degree)
The perimeter of a circular sector
We know a circular sector contains two radii and an arc.
so Perimeter of sector = Arc length + 2×Radius of circle
We know the central angle of a circle is 360°. Let θ is the central angle of the sector
Then Length of arc = (θ/360) × Perimeter of the circle
We Know the perimeter of a circle is 2πr
so, Length of arc = (θ/360)×2πr = θπr/180 (here θ in degree)
Perimeter of sector = 2r + θπr/180
Sample problems
1) if the circle’s radius is 6 cm and the angle of the sector is 60°. then find the area and perimeter of the sector
Area of sector = θπr²/360 = 60×π×6²/360 = 6π cm²
Perimeter of sector = 2r + θπr/180 = 2×6 + 60×π×6/180 = 12 + 2π cm
2) if the area of the circle is 2π cm² and the angle of the sector is 180°. then find the radius and perimeter of the sector
Area of sector = θπr²/360 = 180πr²/360 = ½πr² = 2π cm²
r²= 4 ⇒ r = 2 cm
Perimeter of sector = 2r + θπr/180 = 2 × 2 + 180 × π × 2/180 = 4 + 2π cm
The segment of the circle
A circular segment or circle segment is a portion of a circle enclosed by a chord and an arc
Formation of the circular segment

A circular segment is formed when a circle is cut through its chords. A chord and an arc are both found in a circular segment. From the figure shaded area is a segment of the circle
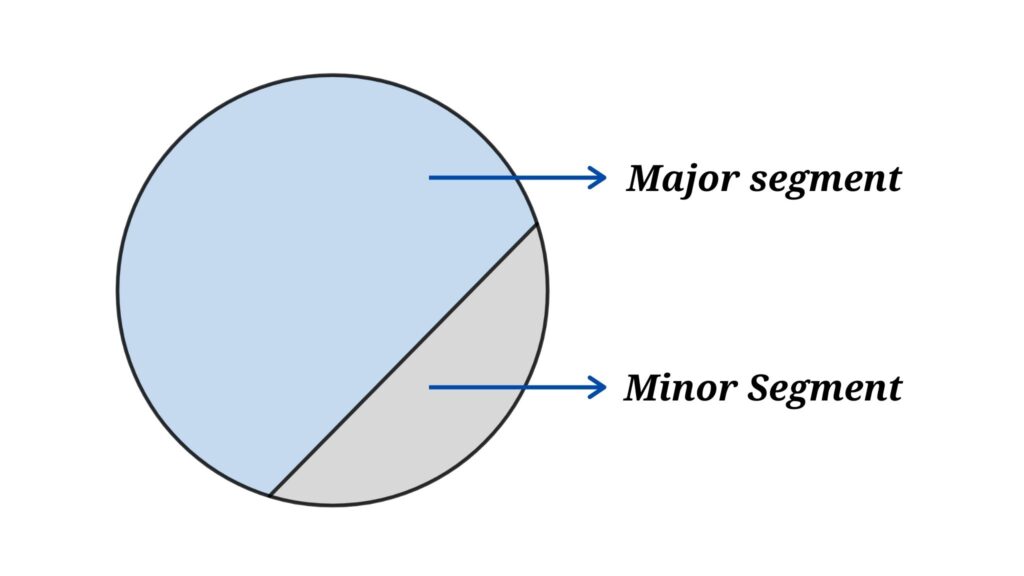
Major segment and minor segment
We saw how to create a circular segment, when we cut a circle through its chord then we will get at least two segments.
Where the smaller area is known as the minor segment and the larger area is the major segment
Area and perimeter of the circular segment
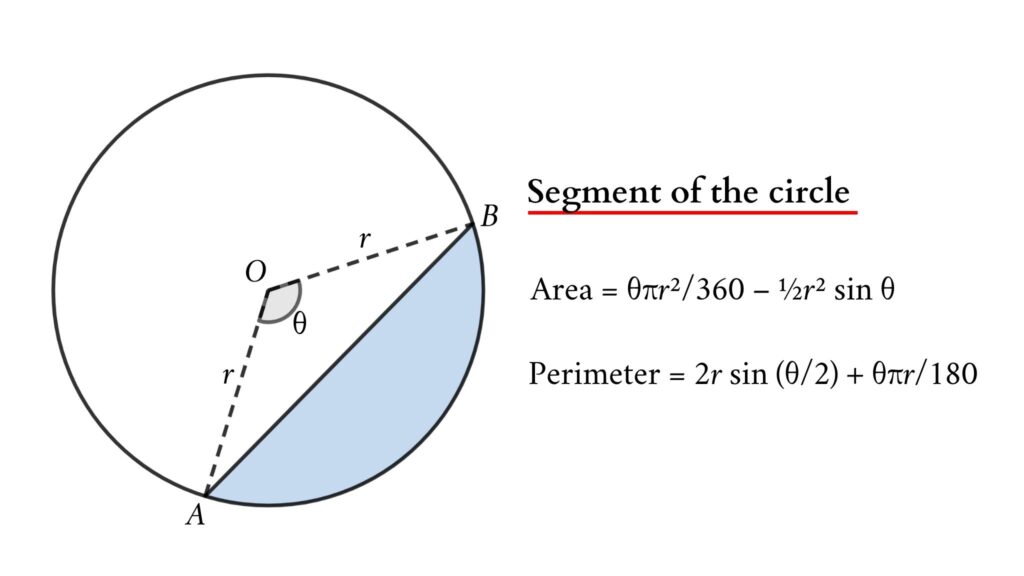
Area of the circular segment
We know the central angle of a circle is 360°. Let θ is the central angle of the arc of the segment
Then the area of the circular segment = Area of the sector (AOB) – Area of ΔAOB
Area of circular segment = (θ/360) × Area of the circle – ½ r² sin θ
We know the area of a circle is πr²
so, Area of segment = (θ/360)×πr² – ½r² sin θ
Area of segment = θπr²/360 – ½r² sin θ (here θ is in degree)
The perimeter of a circular segment
We know a circular segment contains a chord and an arc.
so Perimeter of segment = Arc length + Length of chord
We know the central angle of a circle is 360°. Let θ is the central angle of the sector
Then Length of arc = (θ/360) × Perimeter of the circle
We Know the perimeter of a circle is 2πr
so, Length of arc = (θ/360)×2πr = θπr/180 (here θ in degree)
Here l is the length of the chord we can apply the cosine rule in ΔAOB then
l² = r² + r² – 2r² cos θ = r²(2 – 2cos θ) = 2r² × 2 sin² (½θ)
l = 2r sin (θ/2)
The perimeter of segment = 2r sin (θ/2) + θπr/180
Sample problems
1) if the circle’s radius is 6 cm and the arc angle is 60°. Then find the area and perimeter of the segment
Area of segment = θπr²/360 – ½r² sin θ = 60×π×6²/360 – ½×6² sin 60 = 6π – 9√3 cm²
Perimeter of sector = 2r sin (θ/2) + θπr/180 = 2×6 sin (60/2) + 60×π×6/180 = 6 + 2π cm
1) if the circle’s radius is 12 cm and the arc angle is 120°. Then find the area and perimeter of the segment
Area of segment = θπr²/360 – ½r² sin θ = 120×π×12²/360 – ½×12² sin 60
Area of segment = 48π – 36√3 cm²
Perimeter of segment = 2r sin (θ/2) + θπr/180 = 2×12 sin (120/2) + 120×π×12/180
The perimeter of the segment = 12√3 + 8π cm
