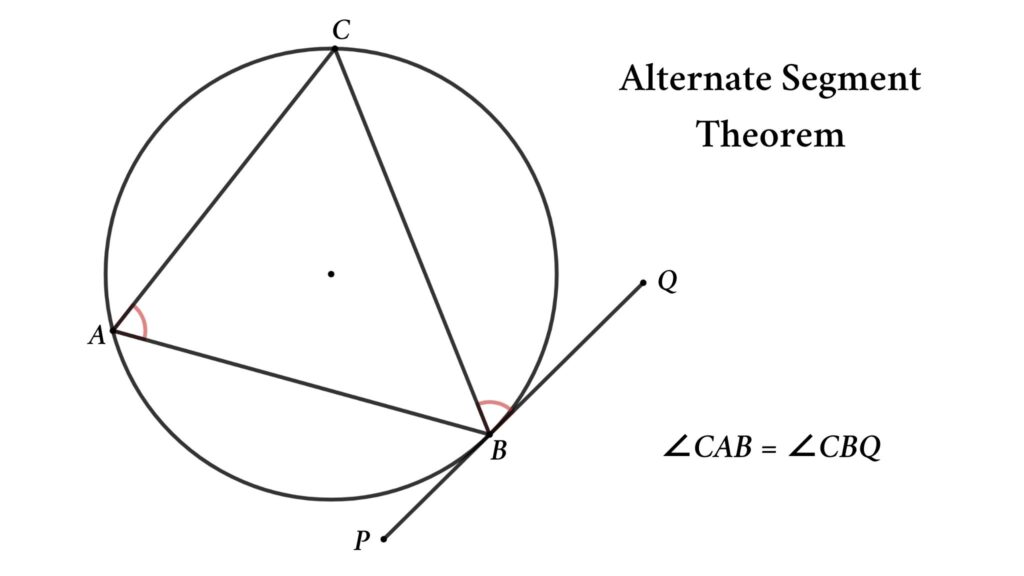
Alternate Segment Theorem In A Circle

Alternate Segment Theorem In A Circle

Alternate segment theorem state that for any circle, the angle formed between the tangent and the chord is equal to the angle formed by the chord in the alternate segment.

For more explanation, from the figure, both the chord CB and the tangent PQ touch at point B and make an angle ∠QBC between them. ∠QBC lies in the small segment of the circle and its alternative segment is BAC so according to the alternate segment theorem we can write ∠CBQ = ∠BAC (here ∠BAC is the angle formed by the chord in the alternate segment)

Proof of Alternate Segment Theorem

Proof of Alternate Segment Theorem
Figure 1

To prove the theorem we need to prove ∠CBQ = ∠CAB

Consider figure 1 and mark the center of the circle as O.

Connect OA and OC.

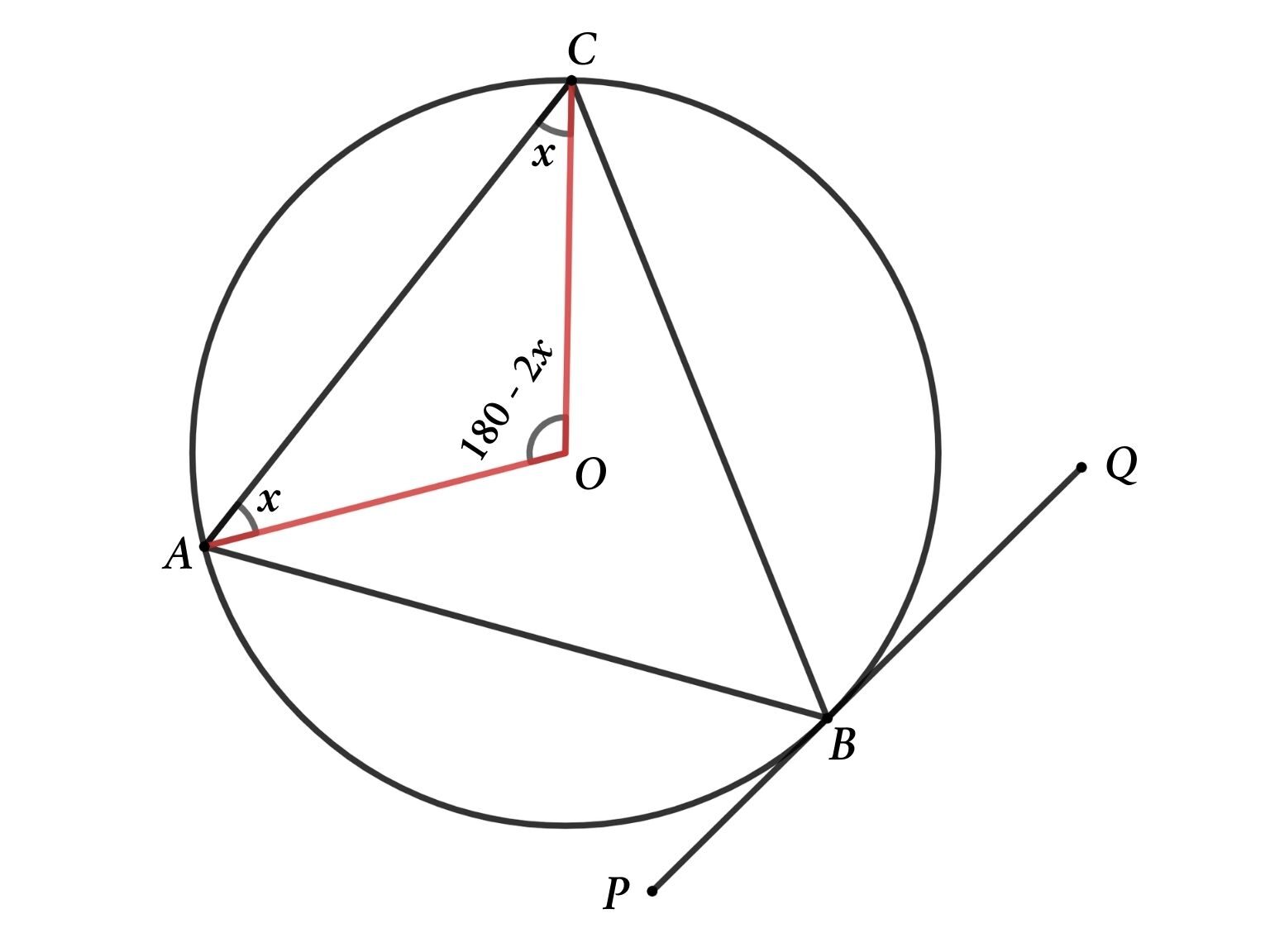
Proof of Alternate Segment Theorem
Figure 2

From figure 2

Consider ∠OAC = x, then ∠OAC = ∠OCA = x because OA = OC = radius of the circle

So, ∠AOC = 180 – (∠OAC + ∠OCA) = 180 – 2x

Now connect OB.

Proof of Alternate Segment Theorem
Figure 3

From figure 3

Consider ∠OCB = y, then ∠OBC = ∠OCB = y because OB = OC = radius of the circle

So, ∠BOC = 180 – (∠OCB + ∠OBC) = 180 – 2y

Figure 4

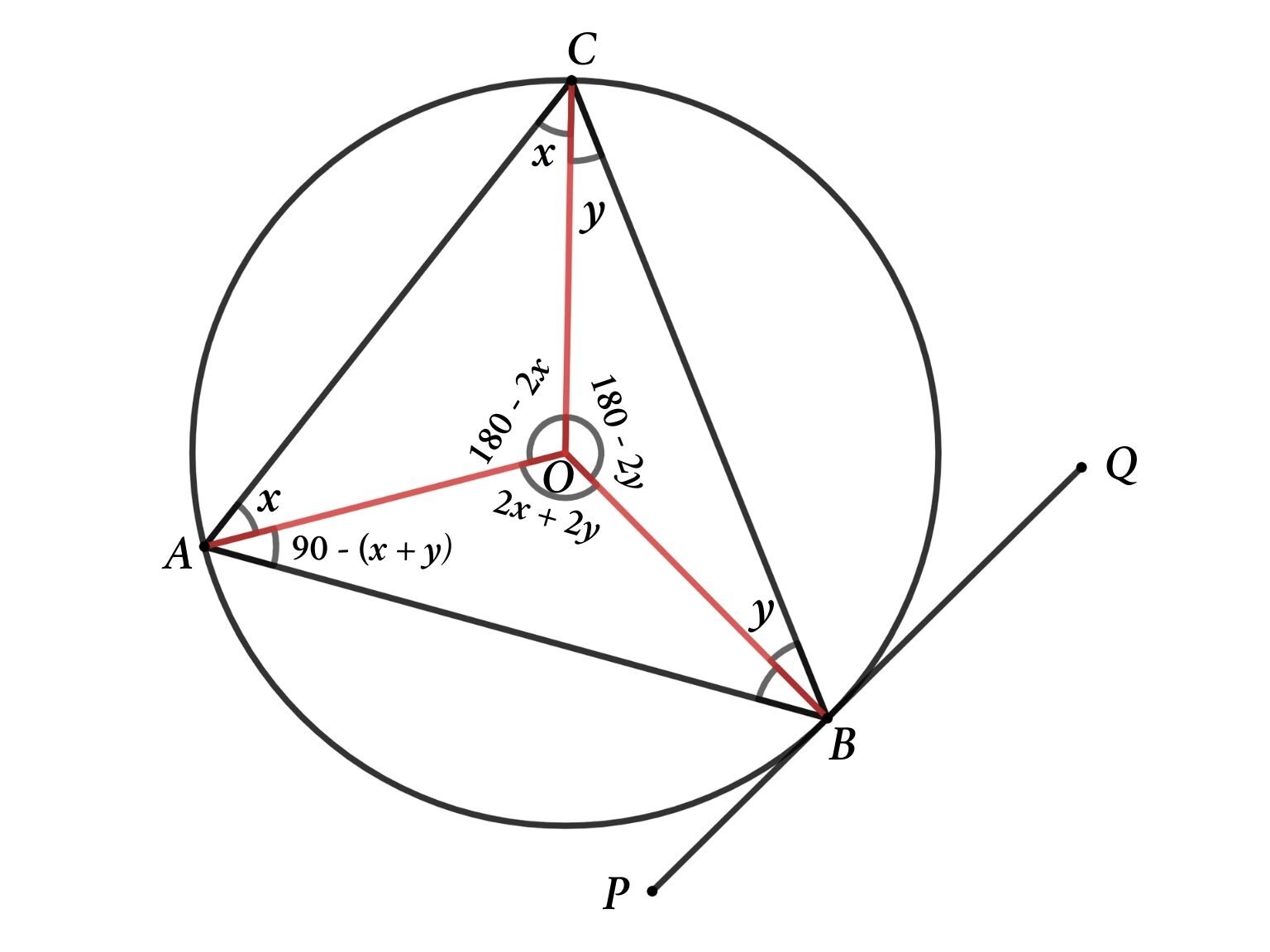
From figure 4

∠AOB = 360 – (∠BOC + ∠AOC) = 360 – (180 – 2x + 180 – 2y) = 2x + 2y

We know OA = OB so ∠OAB = ∠OBA

then ∠OAB = (180 – (2x + 2y))/2 = 90 – (x + y)

Figure 5

From figure 5

∠OBQ = 90° – (OB is the tangent of the circle)

So ∠CBQ = 90 – ∠OBC = 90 – y

∠CAB = x + 90 – (x + y) = 90 – y

That is ∠CBQ = ∠CAB = 90 – y