What is the Area and Perimeter of the Circle?

The region or space a circle takes up in a two-dimensional plane is known as the area of the circle. and it is measured in square units like m², cm², etc.
The perimeter of a shape is the length of its outline. It is usually measured in centimeters (cm), meters (m), or kilometers (km). The term “circumference” is sometimes used instead of “perimeter”.
When we find the area or circumference much like polygons, we can’t multiply the length of a circle’s sides together to find its area or we can’t add the sides to find the perimeter (such as squares, triangles, or parallelograms). Instead, we measure the distance between the circle’s center and edge (radius) or the distance between two edges through its center (diameter). We should be mindful of these two measurements while determining the area and circumference of a circle. Here diameter = 2 × radius
Area and Perimeter of the Circle

| Circle | Quarter circle | Semicircle | |
| Area | π · r² | π · r²/4 | π · r²/2 |
| Perimeter | 2 · π · r | 2 · r + π · r/2 | 2 · r + π · r |
The Perimeter of a Circle Formula
Perimeter or Circumference of a circle = 2 · π · r
where:
r is the radius of the circle
π is Pi, approximately (up to 3 decimals) 3.142
If we know the diameter of the circle then
Perimeter or Circumference of a circle = π · d
where:
d is the diameter of the circle
Area of the Circle Formula
Area of the circle = π · r²
where:
r is the radius of the circle
π is Pi, approximately (up to 3 decimals) 3.142
If we know the diameter of the circle then
Perimeter or Circumference of a circle = π · d²/4
where:
d is the diameter of the circle
Derivation of Area of the Circle
There are several ways to demonstrate that the area of a circle is π · r². I’m going to present four methods here.
- Using the area of the polygon
- Using the area of the triangle
- Using the area of the rectangle
- Using Integration
Using the Area of Polygons
If we draw an Octagon inside the circle.
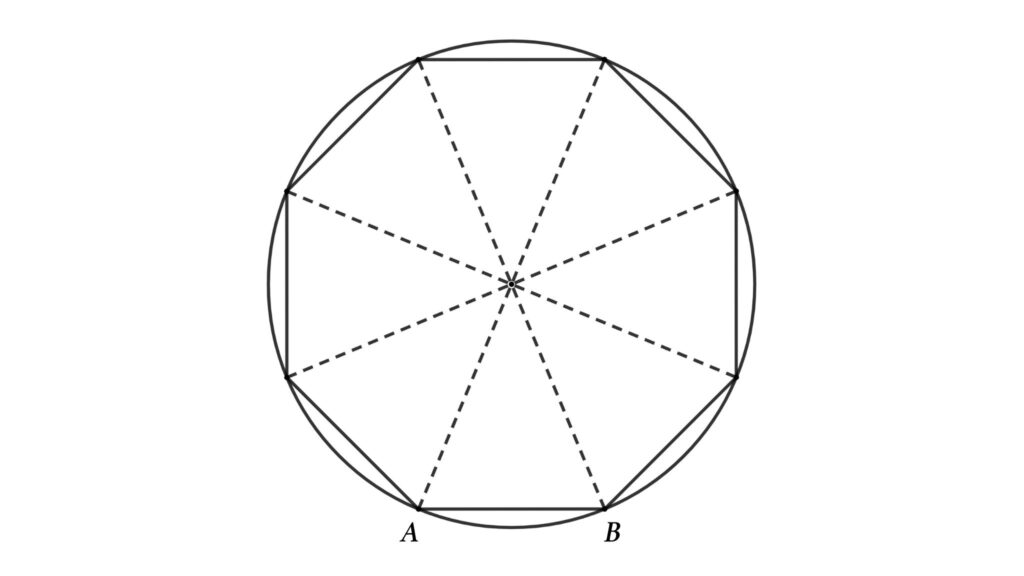
Then the area of the circle is almost equal to the area of the octagon
If we increase the number of sides of the polygon, then the area of the polygon and the circle become closer.
As we increase the polygon’s size, the length of AB approaches zero (not 0). Then we get the most precise circle area.
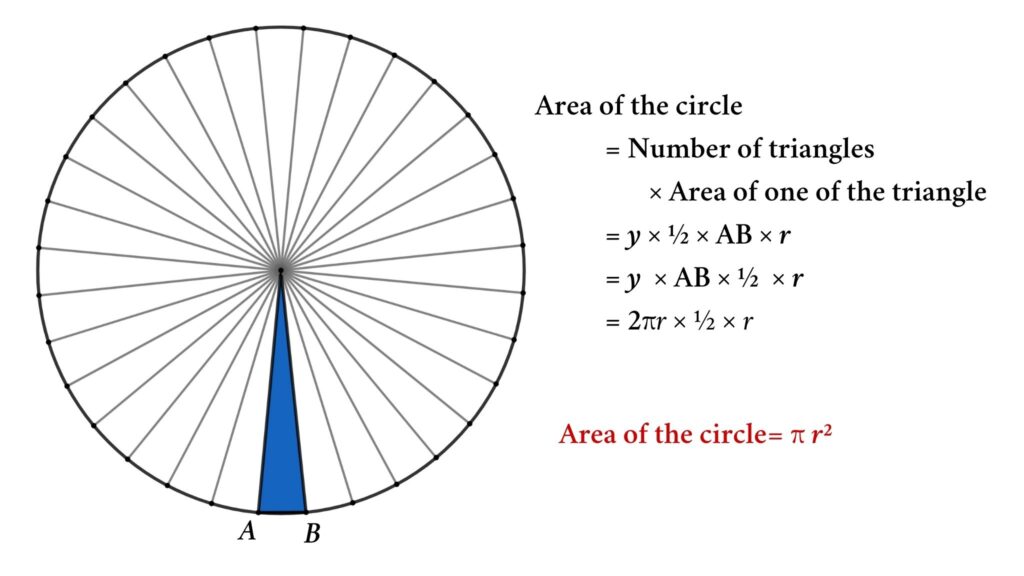
We know how to find the area of the polygons by dividing the polygons into triangles
In this case, Let’s assume the sides of the polygons are y.
If we divide the polynomial as shown in the figure, then the height of the triangle becomes the radius of the circle and we can draw y triangles. Now,
Area of y triangles = Area of the circle
Area of one triangle = ½ × AB × r
Area of y triangles = Area of one triangle × y = ½ × AB × r × y
Here AB × y = circumference of the circle = 2 · π · r
Area of y triangles = ½(2πr) · r = π· r²
That is the area of the circle = π · r²
Using Integration in the Area of Polygon
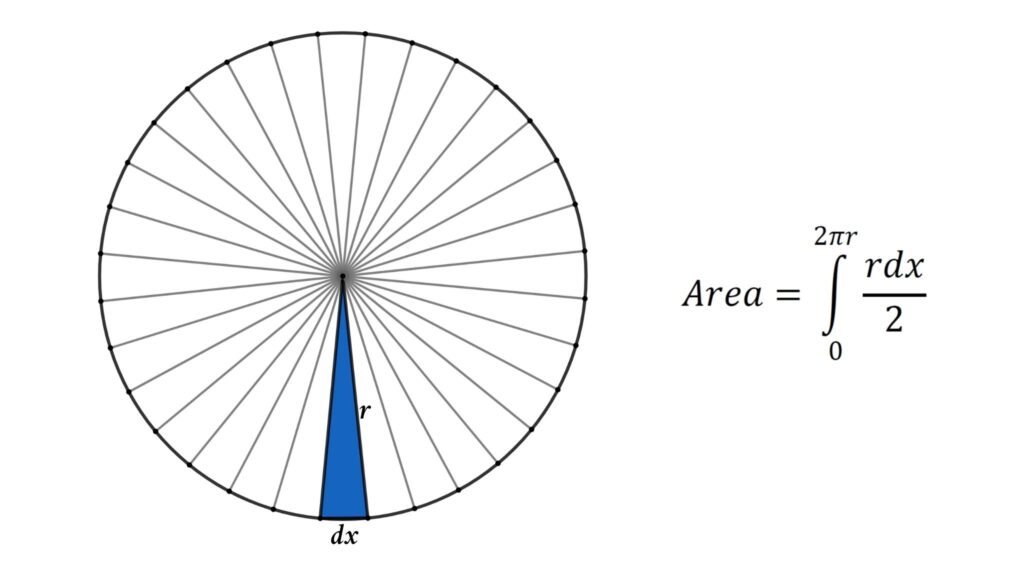
From the geometry method, we saw that AB is tenting to zero so let’s consider AB = dx, so the area of one triangle = ½(dx) · r.
Here we are going to integrate ½(dx)r from zero to 2πr(perimeter of the circle).
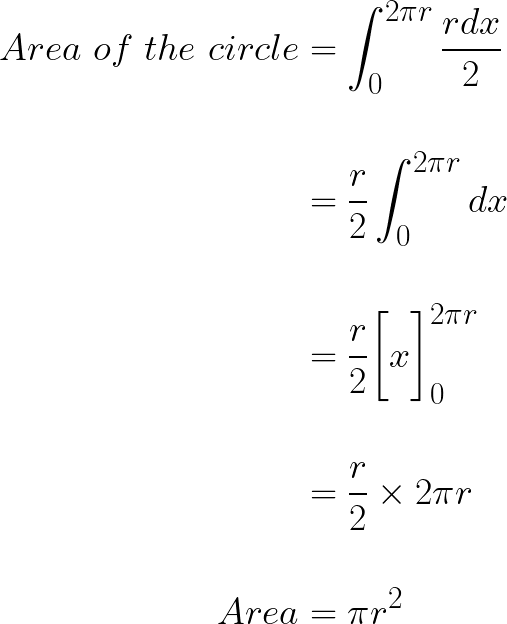
Using the Area of the Triangle
From the figure, let’s assume what happens if we cut and open the circle through its center
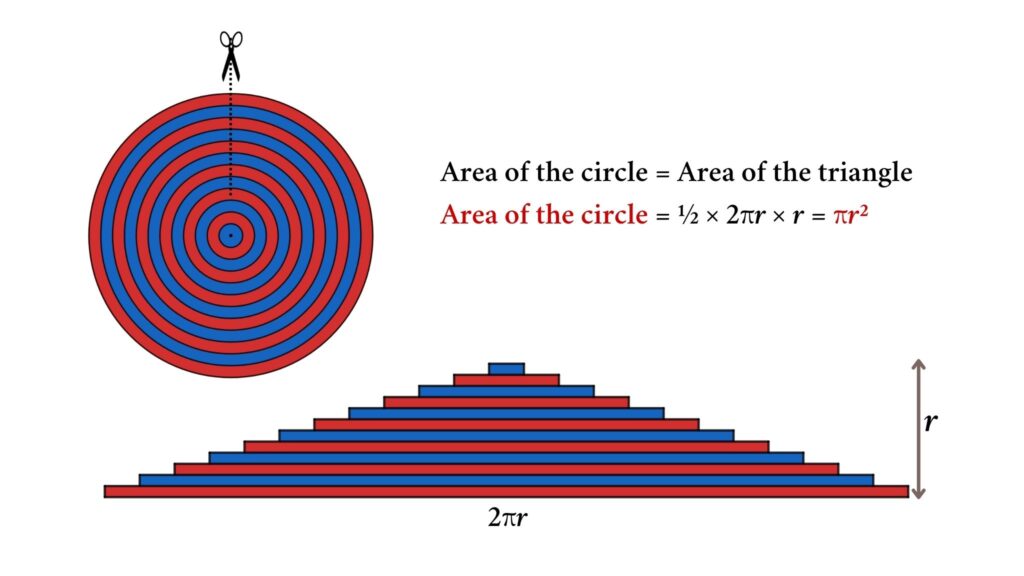
Here we have a new triangle with the base as the parameter of the circle and the height as the radius of the circle
So we get,
Area of the circle = ½ × base × height = ½ × 2π × r = π · r²
Using the Area of the Rectangle

The figure shows a circle divided into 4 sectors and arranged in a certain way. What happens when we increase the number of sectors?
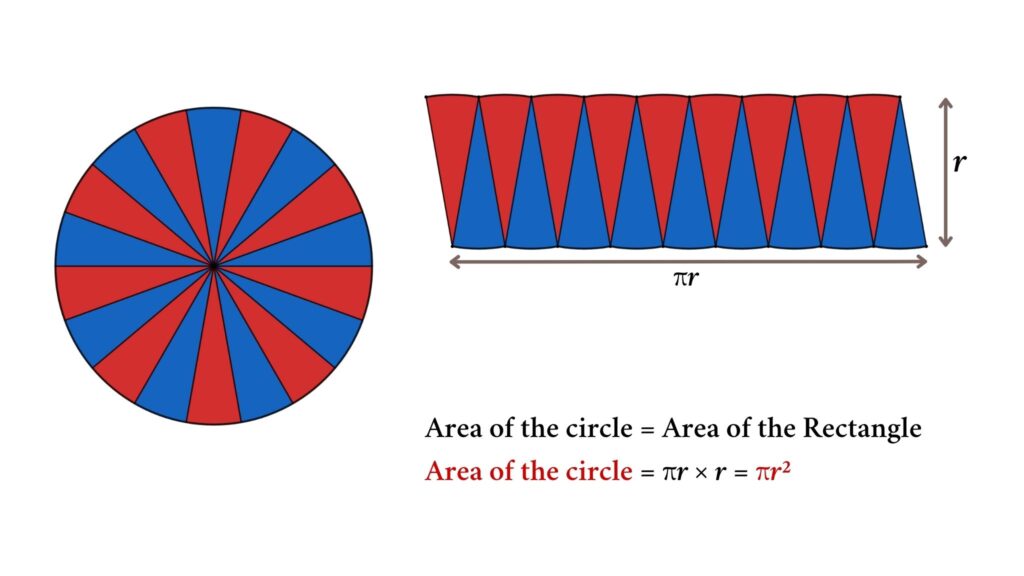
Here we have divided the circle into 18 sectors so the rearrangement looks like more of a rectangle. If we increase the number repeatedly, the figure becomes close to the rectangle with one side half of the perimeter and another circle’s radius. So,
Area of the circle = Area of the rectangle = base × height
Area of the circle = π · r × r = π · r²
Using Integration
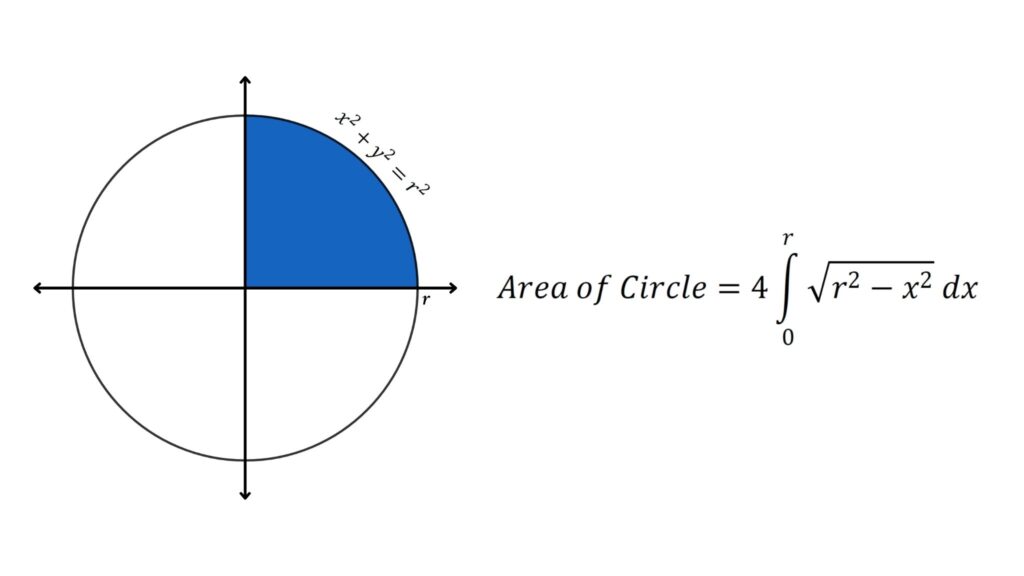
We can also use the area under the curve to find the area of the circle. We divide the circle into 4-quarter circles by using integration we can find the area of a quarter circle.

Area and Perimeter of a Quarter Circle Formula
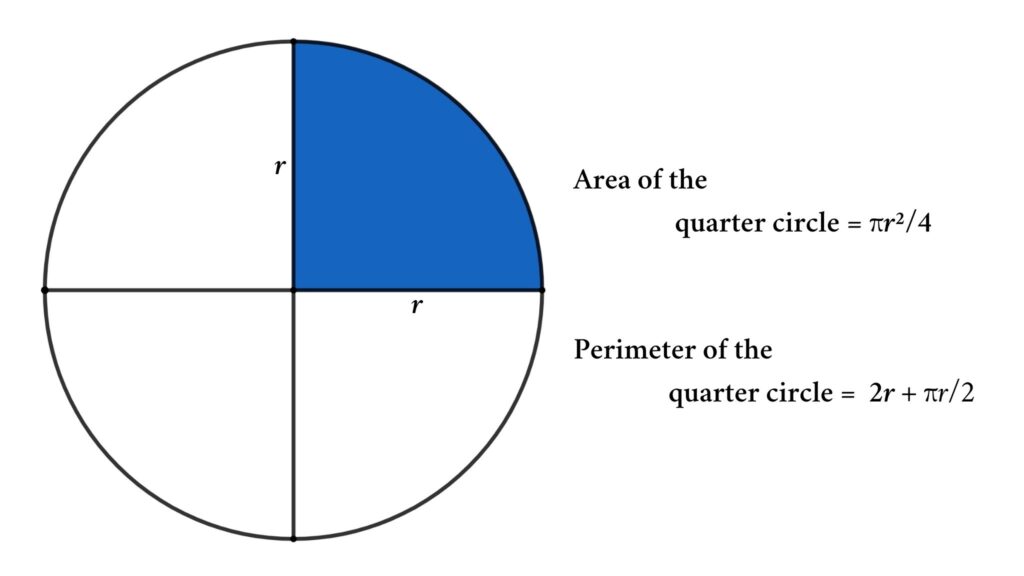
We know that a quarter circle is one by fourth of the circle
So, the Area of the quarter circle = π · r²/4 or π · d²/16 (where r is the radius and d is the diameter)
However, when calculating the perimeter, we must also consider the radius on the sides of the quadratic circle.
So, the perimeter of the quarter circle is 2r + π · r/2 or d + π · d/4
Area and Perimeter of a Semicircle Formula

We know that a semicircle is half of the circle, Area of the quarter circle is πr²/2 or πd²/8 (where r is the radius and d is the diameter)
However, when calculating the perimeter, we must also consider the radius on the sides of the quadratic circle.
So, the perimeter of the quarter circle is π · r + 2r or π · d/2 + d
Sample Problems
1) If the circle’s diameter is 10 cm then what is the area of the circle?
Diameter (D) = 2 × Radius(r) = 10 cm
Area = π · r² = π(½d)² = π(5)² = 25π cm²
2) If the perimeter of the circle is 2π cm then find the area.
Perimeter = 2π · r = 2π cm
That is r = 1 cm
Area = π · r² = π(1)² = π cm²
3) If the perimeter of a quarter circle is 4 + π cm then find the radius.
Perimeter = 2r + π · r/2 = 4 + π cm
That is r = 2 cm
