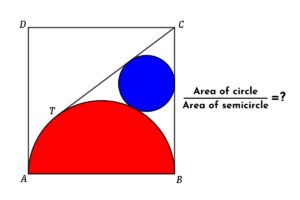
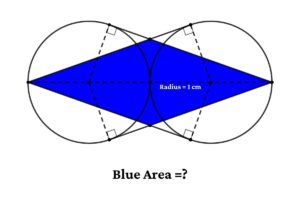
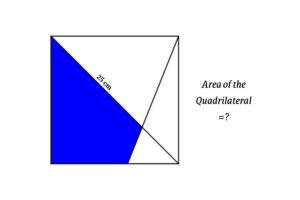
Find the Area of a five-pointed star which is inscribed inside a regular pentagon with sides of 8 cm
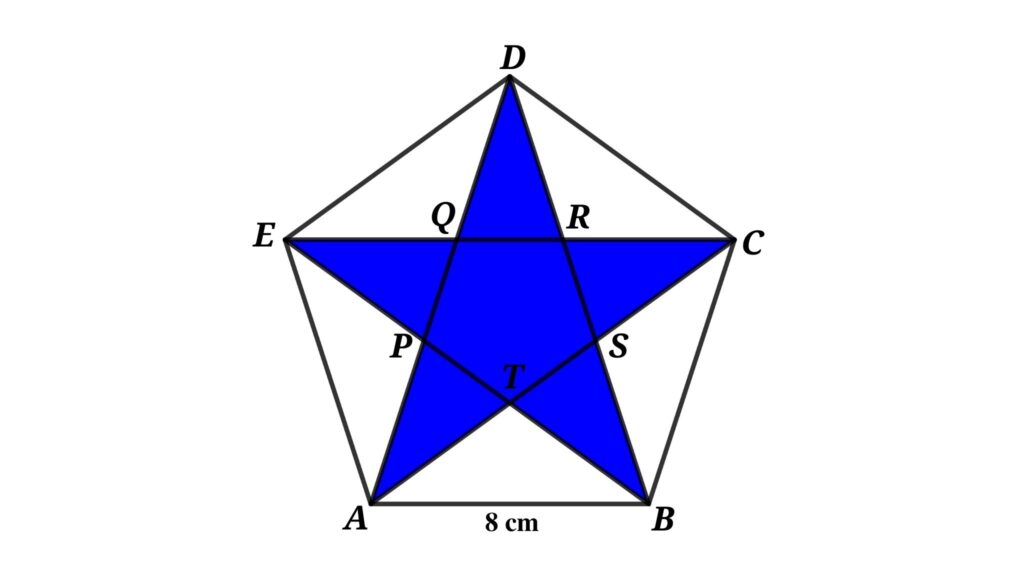
Solution: Area of the Star
Area of the star = Area of the pentagon – Area of the five white triangles
We can divide a regular pentagon into five equal triangles as shown below, where O is the center of the pentagon

From figure
Area of the Pentagon = 5 × Area of the triangle AOB
∠OBA = ∠OBC = 108/2 = 54°
⇒ ∠OAB = 54°
∠AOB = 180 – (∠OBA + ∠OAB)
⇒ ∠AOB = 180 – (54 + 54) = 72°
Apply the sine rule in triangle AOB
AO / sin ∠OBA = AB / sin ∠AOB
\( \Rightarrow AO = \dfrac{AB \times \sin ∠OBA}{\sin ∠AOB} \)
\( \Rightarrow \ AO=\dfrac{8 \times \sin 54}{\sin 72} \)
\( \Rightarrow \ AO=\dfrac{8 \times \dfrac{\sqrt{5}+1}{4}}{\dfrac{\sqrt{10+2\sqrt5}}{4}} \)
\( \Rightarrow \ AO=\dfrac{8 \times (\sqrt{5}+1)}{\sqrt{10+2\sqrt5}} \)
\( \Rightarrow \ AO=\dfrac{8\sqrt{5}+8}{\sqrt{10+2\sqrt5}} \ \mathrm{cm} \)
\( \mathrm{Area\ of \ the\ triangle \ AOB} = \dfrac{1}{2}\times AB \times AO \times \sin 54 \)
\( \Rightarrow \ \mathrm{Area\ of \ the\ triangle \ AOB} = \dfrac{1}{2}\times 8 \times \dfrac{8\sqrt{5}+8}{\sqrt{10+2\sqrt5}} \times \dfrac{\sqrt{5}+1}{4} \)
\( \Rightarrow \ \mathrm{Area\ of \ the\ triangle \ AOB} = \dfrac{48+16\sqrt{5}}{\sqrt{10+2\sqrt5}} \ \mathrm{cm^2} \)
\( \Rightarrow \ \mathrm{Area\ of \ the\ pentagon} = 5 \times \dfrac{48+16\sqrt{5}}{\sqrt{10+2\sqrt5}} \ \mathrm{cm^2} \)
\( \Rightarrow \ \mathrm{Area\ of \ the\ pentagon} = \dfrac{240+80\sqrt{5}}{\sqrt{10+2\sqrt5}} \ \mathrm{cm^2} \)
\( \Rightarrow \ \mathrm{Area\ of \ the\ pentagon} = \dfrac{240+80\sqrt{5}}{\sqrt{10+2\sqrt5}} \times \dfrac{\sqrt{10-2\sqrt5}}{\sqrt{10-2\sqrt5}} \)
\( \Rightarrow \ \mathrm{Area\ of \ the\ pentagon} = \dfrac{240\sqrt{10-2\sqrt5}+80\sqrt{5} \times \sqrt{10-2\sqrt5}}{4\sqrt{5}} \)
\( \Rightarrow \ \mathrm{Area\ of \ the\ pentagon} = {12\sqrt{5} \times \sqrt{10-2\sqrt5}+20\sqrt{10-2\sqrt5}} \)
\( \Rightarrow \ \mathrm{Area\ of \ the\ pentagon} = {12 \sqrt{50-10\sqrt5}+20\sqrt{10-2\sqrt5}} \)
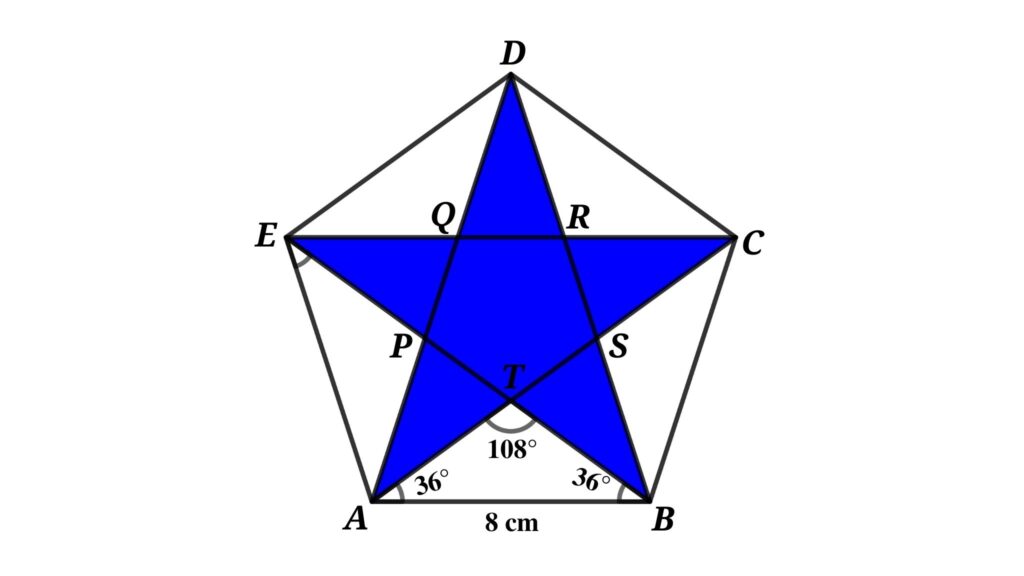
From Figure
∠ATB = ∠ATB = 108°
Then
∠TAB = ∠TBA = (180 – 108)/36 = 72/2 = 36°
Apply the sine rule in triangle ABT, then
AT / sin ∠TBA = AB / sin ∠ATB
\( \Rightarrow \ AO=\dfrac{AB \times \sin ∠OBA}{\sin ∠AOB} \)
\( AT=\dfrac{AB \times \sin ∠TBA}{ \sin ∠ATB} \)
\( \Rightarrow AT=\dfrac{8 \times \sin 36}{ \sin 108} \)
\( \Rightarrow AT=\dfrac{8 \times \dfrac{\sqrt{10-2\sqrt5}}{4}}{ \dfrac{\sqrt{10+2\sqrt5}}{4}} \)
\( \Rightarrow AT=\dfrac{8 \times \sqrt{10-2\sqrt5}}{\sqrt{10+2\sqrt5}} \)
\( \Rightarrow AT=8 \times \sqrt{\dfrac{(10-2\sqrt5)(10-2\sqrt5)}{(10+2\sqrt5)(10-2\sqrt5)}} \)
\( \Rightarrow AT=8 \times {\dfrac{10-2\sqrt5}{4\sqrt{5}}} \)
\( \Rightarrow AT={\dfrac{20-4\sqrt5}{\sqrt{5}}} \)
\( \Rightarrow AT=4\sqrt5-4 \)
\( \mathrm{Area\ of \ the\ triangle \ ABT} = \dfrac{1}{2}\times AB \times AT \times \sin 36 \)
\( \Rightarrow \mathrm{Area\ of \ the\ triangle \ ABT} = \dfrac{1}{2}\times 8 \times (4\sqrt5-4) \times \dfrac{\sqrt{10-2\sqrt5}}{4} \)
\( \Rightarrow \mathrm{Area\ of \ the\ triangle \ ABT} =(4\sqrt5-4) \times \sqrt{10-2\sqrt5} \)
\( \Rightarrow \mathrm{Area\ of \ the\ 5 \ White \ triangles} =20\sqrt{50-10\sqrt5}-20\sqrt{10-2\sqrt5} \ \mathrm{cm^2} \)
Area of the star = Area of the pentagon – Area of the five white triangles
\( \Rightarrow \mathrm{Area\ of \ the\ star} ={12 \sqrt{50-10\sqrt5}+20\sqrt{10-2\sqrt5}} -(20\sqrt{50-10\sqrt5}-20\sqrt{10-2\sqrt5}) \)
\( \Rightarrow \mathrm{Area\ of \ the\ star} =40\sqrt{10-2\sqrt5}-8 \sqrt{50-10\sqrt5} \ \ \mathrm{cm^2} \)
That is
Area of the star ≈ 51.987 cm²