What is the area of the triangle inside the circle and the radius of the circle?
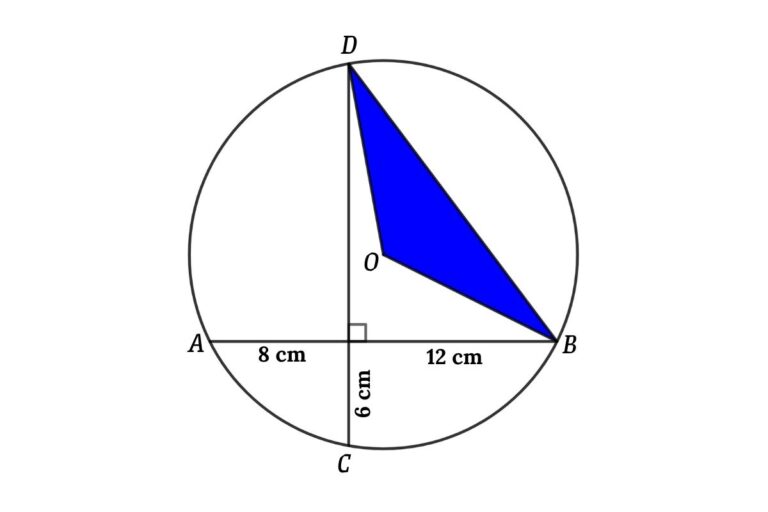
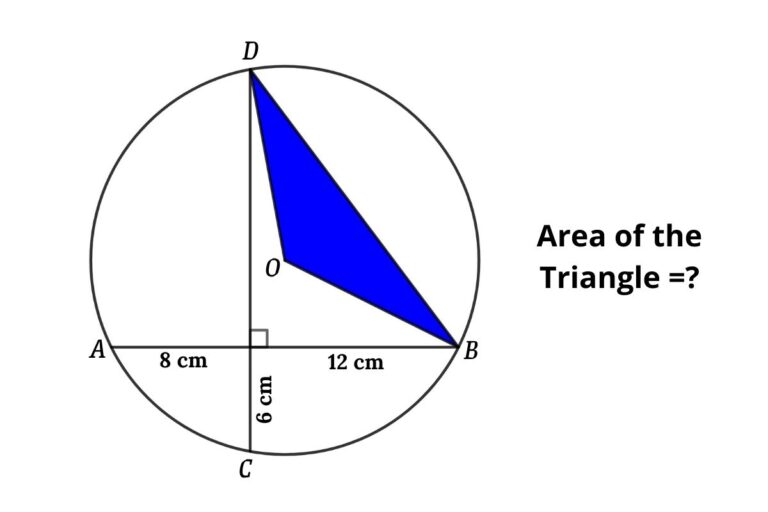
From the figure, AB and CD are chords of the circle and both chords are perpendicular to each other, then find the radius of the circle and area of the blue triangle if O is the center of the circle.
Solution: Radius of the circle and area of the triangle
To find the area of the triangle inside the circle we need to find the radius of the circle

From the figure
Apply the chord intersection theorem
MA × MB = MC × MD
⇒ 8 × 12 = 6 × MD
⇒ MD = 16 cm
Connect OB and OP, and then we can form the triangle POB
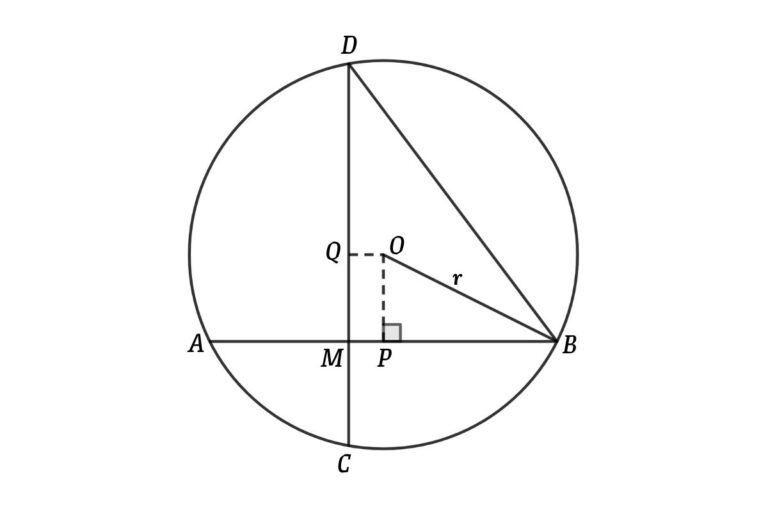
Let the radius of the circle be r
From figure
CD = MC + MD = 6 + 16 = 22 cm
AB = MA + MB = 8 + 12 = 20 cm
Apply Pythagorean theorem in triangle POB
OB² = OP² + BP²
Where, OP = QM = CD – (MC + QD)
QD = CD/2 = 22/2 = 11 cm
Now, OP = 22 – (6 + 11) = 5 cm
BP = AB/2 = 20/2 = 10 cm
Then, OB² = 5² + 10²
⇒ r² = 25 + 100
so, r² = 125
⇒ r = 5√5 cm
so, the radius of the circle = 5√5 cm
We know MD = 16 cm, then we can find BD from the figure using the Pythagorean theorem
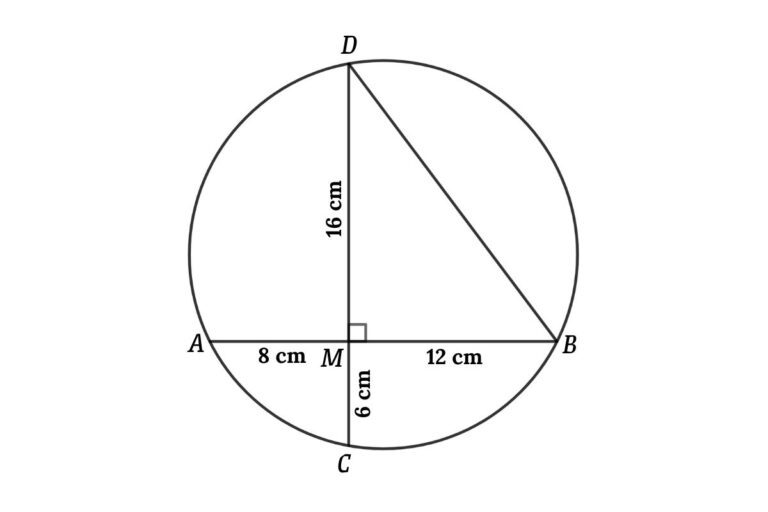
Apply Pythagorean theorem in triangle BMD
BD² = MB² + MD²
⇒ BD² = 12² + 16²
⇒ BD² = 144 + 256
then, BD² = 400
⇒ BD = 20 cm
Connect OF

Apply Pythagorean theorem in triangle OFB
OF² = BO² + BF²
⇒ OF² = (5√5)² – 10²
⇒ OF² = 125 – 100
thus, OF² = 25
⇒ BD = 5 cm
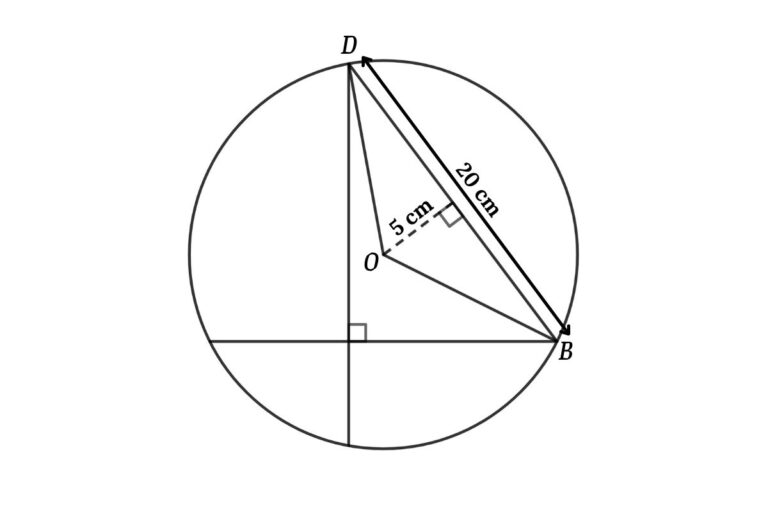
Now area of the triangle = ½ × 20 × 5
⇒ Area of the triangle = 50 cm²