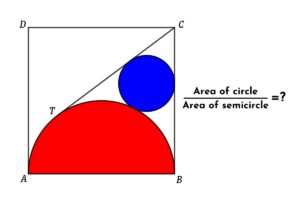
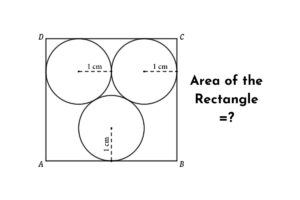
Geometry Math Problem: Find the area of the kite when the sides of the kite are tangents and radii of the circle
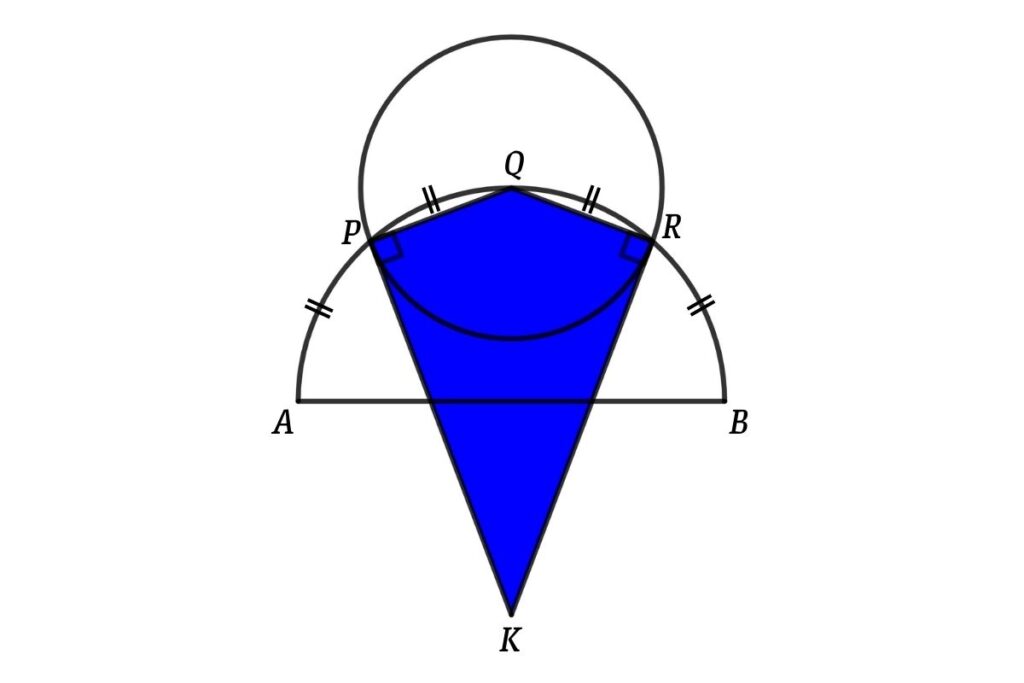
From figure AB = 4 cm and arc AP = PQ = QR = RB. PQ and QR are radii of the circle and PK and RK are tangents of the circle. Then find the area of the kite PQRK
Solution
We select the semicircle and connect PO, QO and RO
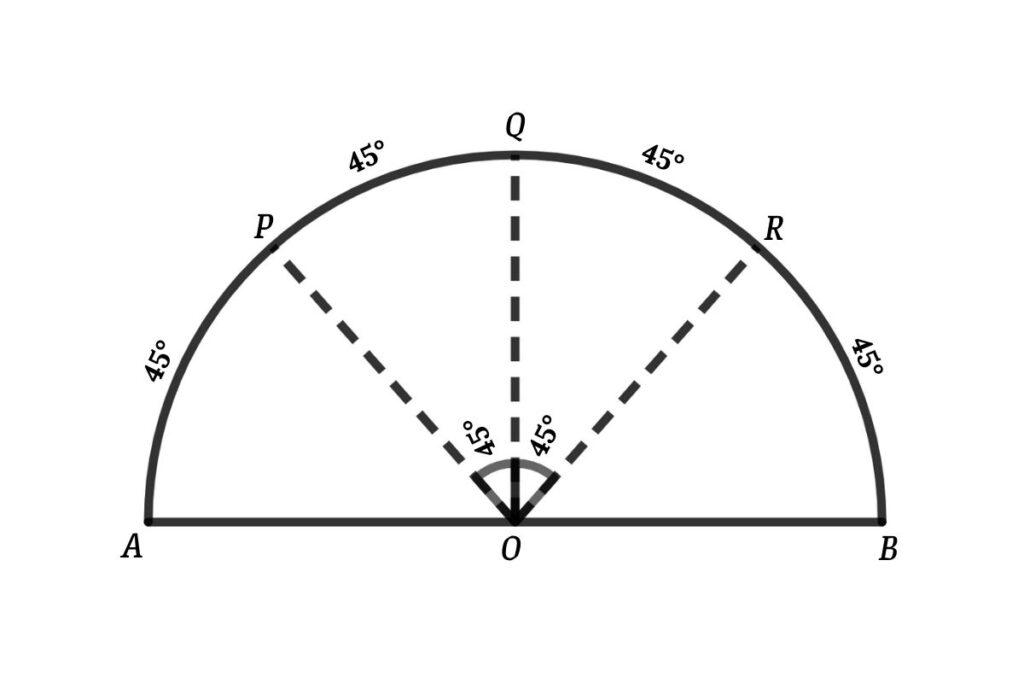
Here
arc AP, PQ, QR and RB equal so
arc AP = arc PQ = arc QR = arc RB = 180/4 = 45°
⇒ ∠POQ = ∠QOR = 45°
Now connect QR then we get the triangle OQR
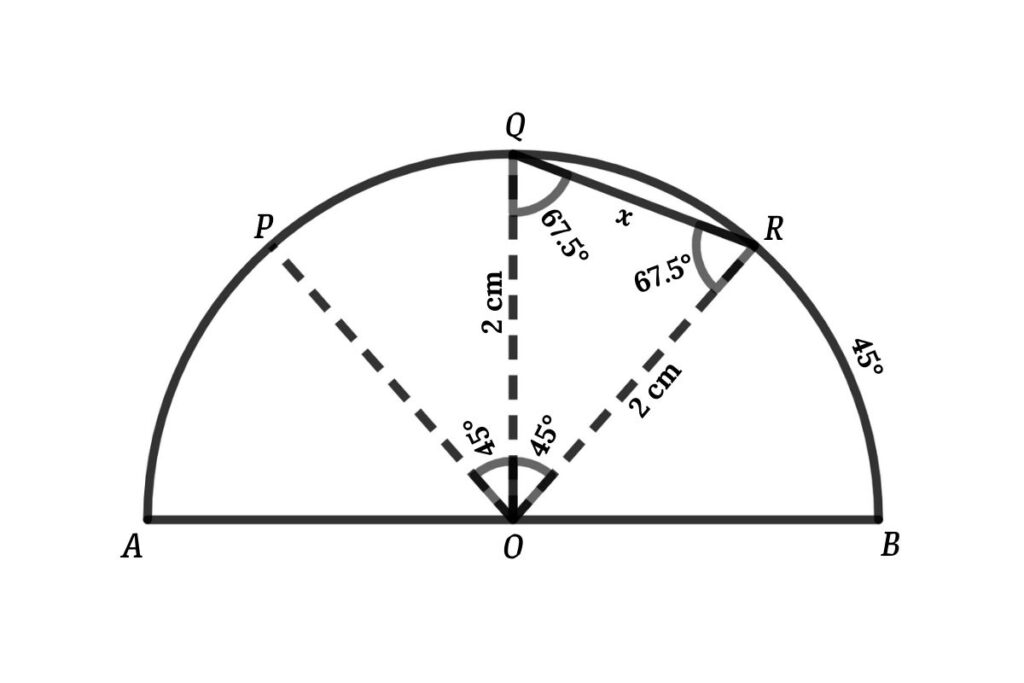
From triangle OQR
∠OQR = ∠ORQ {QO = RO}
⇒ ∠OQR = ∠ORQ = (180 – 45)/2
⇒ ∠OQR = ∠ORQ = 67.5°
Let QR = x
Apply cosine rule in the triangle in OQR
QR² = QO² + RO² – 2 × QO × RO × cos 45°
⇒ x² = 2² + 2² – 2 × 2 × 2 × 1/√2
⇒ x² = 4 + 4 – 4√2
Thus, x² = 8 – 4√2
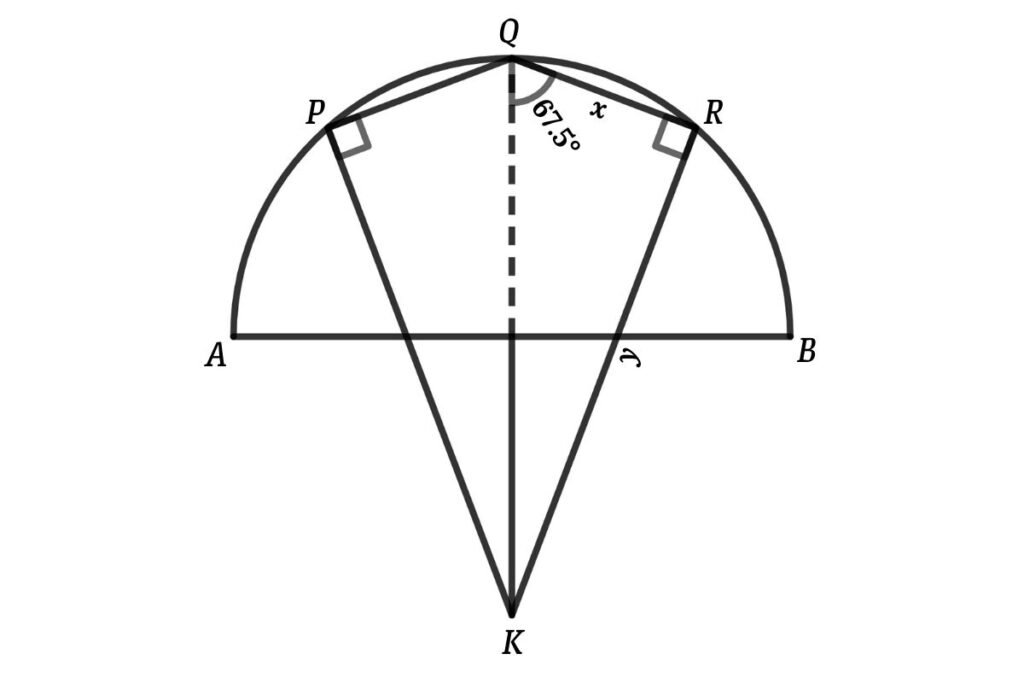
From figure area of the kite = 2 × Area of the triangle KQR {since ΔKQR and ΔKPQ are congruent triangles}
From triangle KQR
Let KR = y, then
tan ∠KQR = KR/QR
⇒ sin 67.5° = y/x
⇒ y = x tan 67.5°
thus, y = x(√2+1)
so, the area of the triangle KQR = ½ × QR × KR
⇒ Area of the triangle KQR = ½ × x × x(√2+1)
⇒ Area of the triangle KQR = ½ × x² × (√2+1)
so, Area of the triangle KQR = ½ × (8 – 4√2) × (√2+1)
⇒ Area of the triangle KQR = (4 – 2√2) × (√2+1)
Thus, the Area of the triangle KQR = 2√2 cm²
Now the area of the kite = 2 × 2√2
⇒ Area of the kite = 4√2 cm²