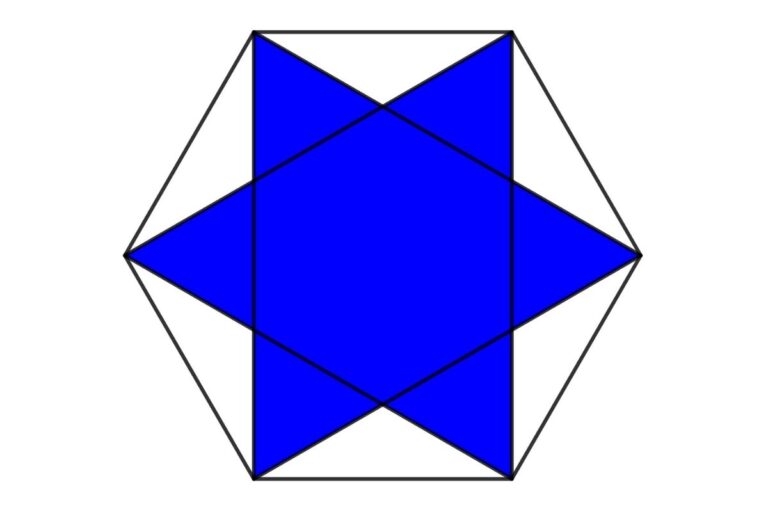
Geometry Math Problem: Find the area of a six-pointed star that is inscribed inside a regular hexagon
The figure shows a star that is inscribed inside a regular hexagon. If the sides of the regular hexagon are 10 cm then find the area of the six-pointed star
Solution
Previously we discussed the area of the five-point star. Here we can solve the problem with the use of symmetry
We can divide the star into 12 equal triangles also all triangles are equilateral triangles
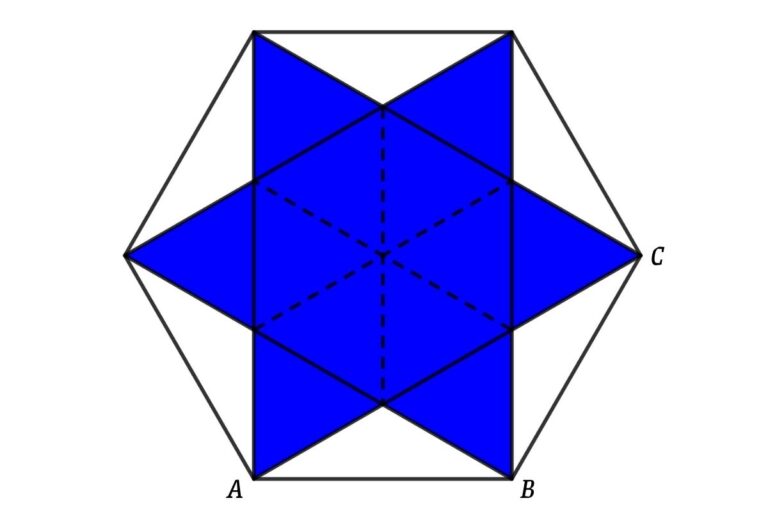
From figure
Area of star = 12 × areas of Triangles
Side of triangle = AC/3
∠ABC = 120°
To find AC apply the cosine rule in ∆ABC
AC² = AB² + BC² – 2×AB×BC×cos 120
⇒ AC² = 100 + 100 – 2×10×10× (-½)
⇒ AC² = 300
Thus, AC = 10√3
So side of triangle = 10√3 /3
⇒ Sides of the triangle = 10/√3
Area of triangle = √3 × (10/√3)²/4
⇒ Area of the triangle = 25/√3 cm²
Then the area of star = 12 × 25/√3
⇒ Area of star = 100√3 cm²