The area under the curve is the area between the curve and the x-axis.
Table of Content
- Area under the curve
- Area between two curves
- Curve under x-axis
- Area between the curve and the y-axis
How to Find the Area Under the Curve?
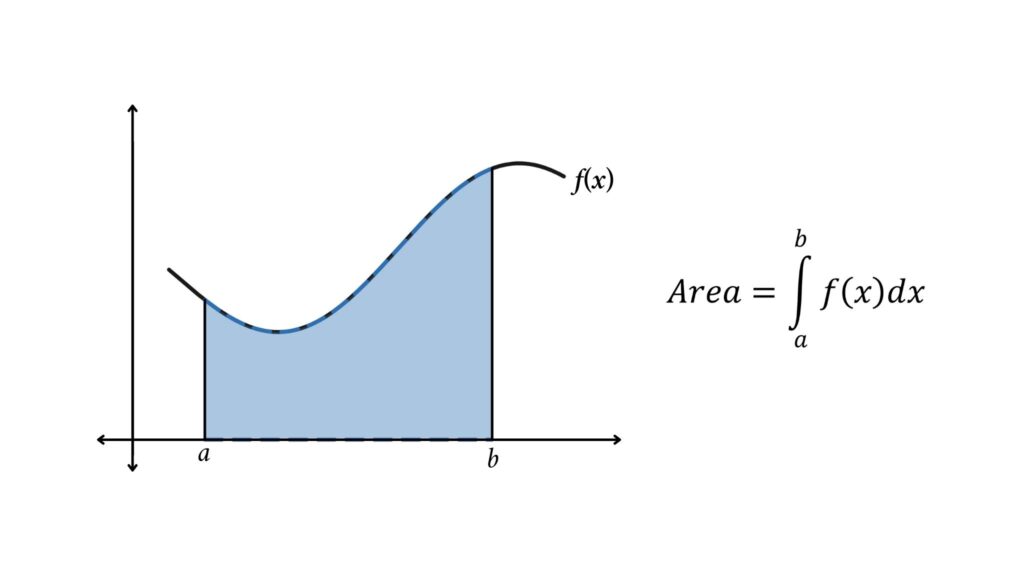
The area under the curve is calculated by performing a definite integration from the starting point to the endpoint. From the figure, to calculate the area under the curve, we will integrate the curve’s equation (f(x)) between the limit points (a & b), where a and b are x coordinates.
So we get the formula for the area under the curve is
$$ \int_{a}^{b} f(x) dx $$
According to the equation, to find the area under the curve, we must first know the curve’s equation, which should be in the form y = f(x)
For example, the below figure represents the curve xy = x + y + 9 in the first quadrant. Calculate the area under the curve within the range of 3 to 9.
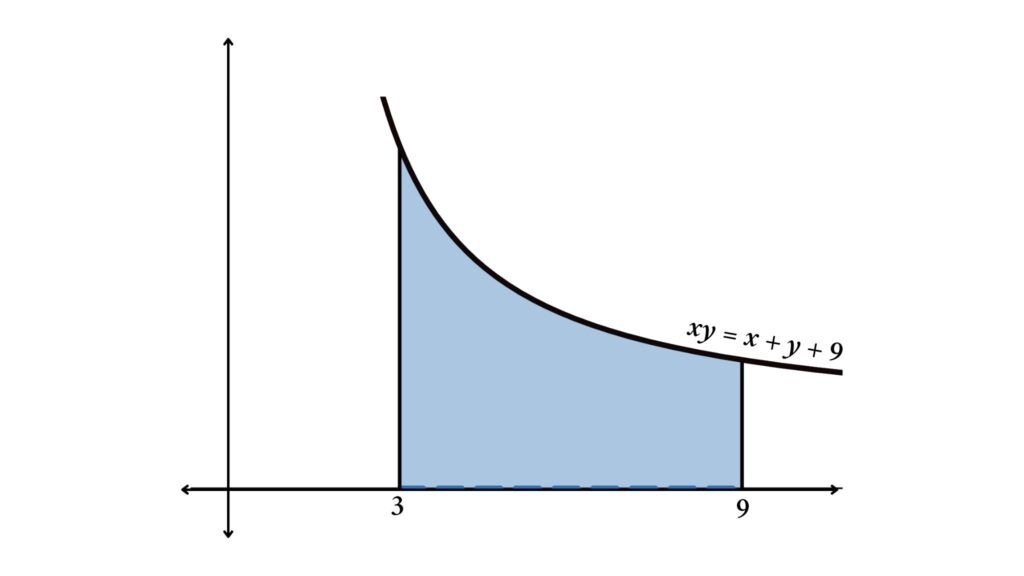
Because the curve’s equation is not in the form y = f(x), we cannot directly find the area under the curve by integration, but we can rearrange the curve’s equation to the form y = f(x), How?
xy = x + y + 9
y = f(x) = (x + 9)/(x – 1)
So the area under the curve is

The Area Between the Two Curves
If we need to find the area between two curves, we must first determine the area under the curve of both curves and then find the differences.
There are three types of scenarios
- Curves are not intersecting
- Curves intersecting or crossing each other
- Curves intersecting or crossing at two points
Area Bonded by Two Curves: Curves are Not Intersecting
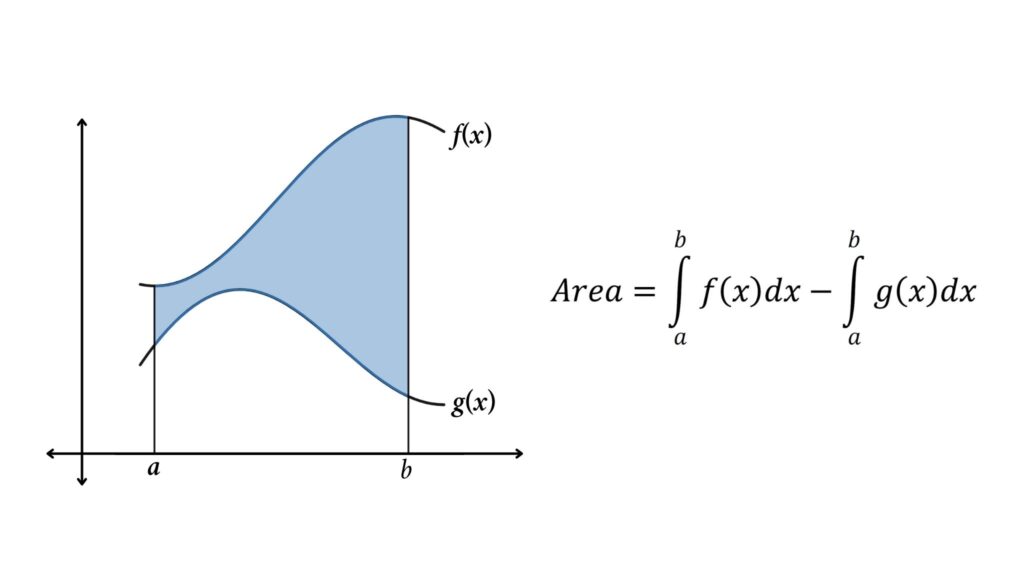
Steps for calculating the area bounded by two curves
- Determine the area under both curves.
- Compute the difference between the curve’s areas under the curve.
- Take the modulus value of the final result to find the area between the two curves.
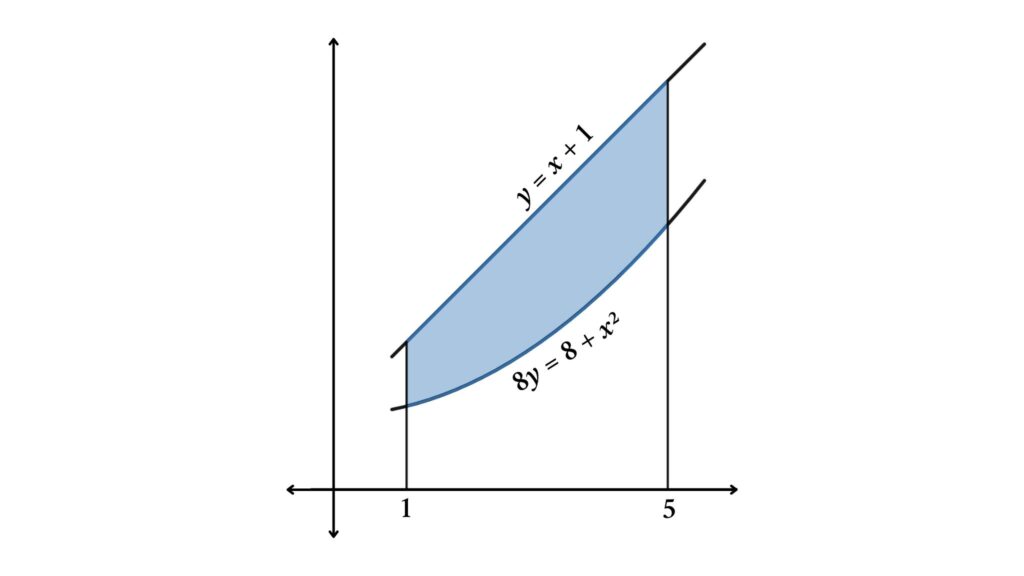
For example, consider the figure below, we need to find the area between the curves from the limit 1 to 5
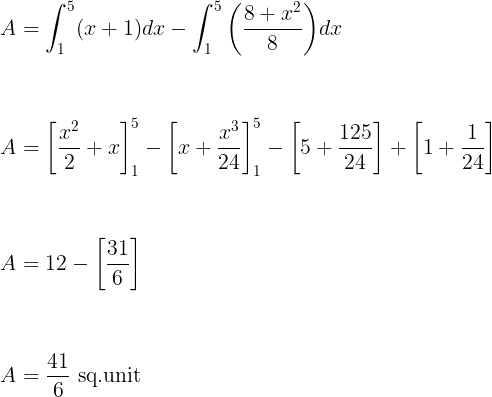
Area Bonded by Two Curves: Curves Intersecting or Crossing Each Other
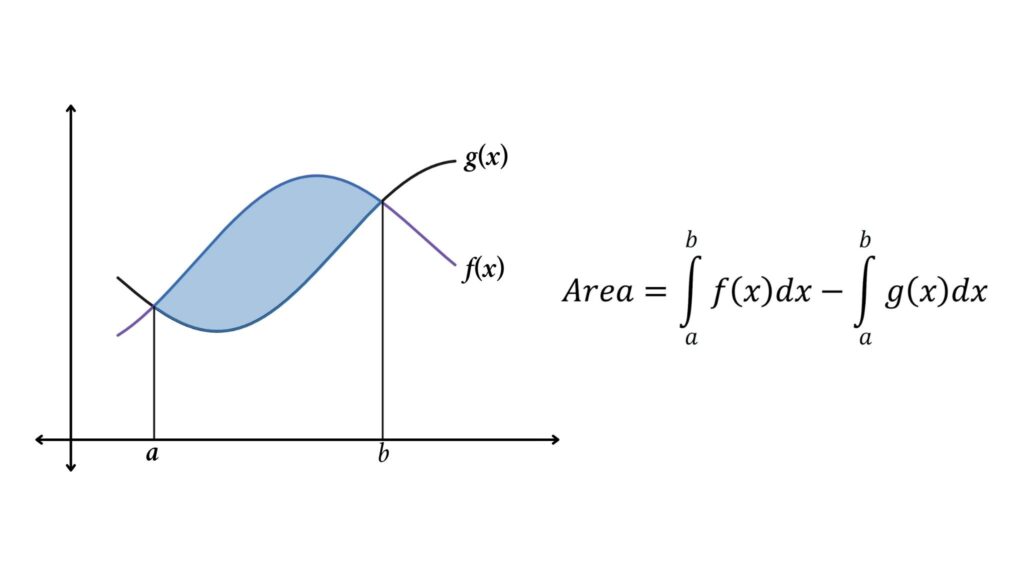
When two curves intersect, the region is divided into several portions from the intersection points, and the area bounded by two curves is given by the sum of the areas of each portion. If there is only one intersection, the region is divided into two parts: the starting point to the intersection point and the intersection point to the endpoint. If there are two intersections, we will divide the region into three portions, and so on. (If there are n intersections, we will divide the region into n + 1)

From the figure both f(x) and g(x) cross at c in the figure, we will find the area between the curves by dividing the blue region into two potions, a to c and c to b. where a is the starting point, b endpoint, and c is the point of intersection
Steps for calculating the area between two intersecting or crossing curves
- Determine the area between the curves from a to c.
- Determine the area between the curves from c to b.
- To calculate the area, add the modulus of the first two steps.
For example, from 1 to 4, determine the area between the curves y = 4 + cos x and y = 4 + sin x.
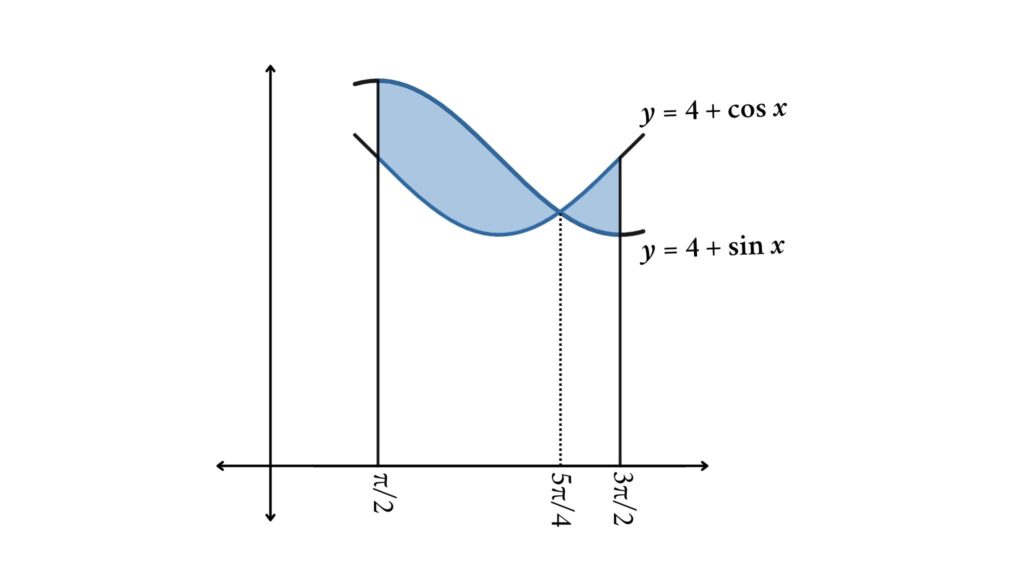
Here first we need to find the intersection points between the curves (We only have one intersection point, so once we find it, we can divide the blue region into two potions.)
y = 4 + cos x = 4 + sin x
cos x = sin x, where x is between π/2 and 3π/2, so
x = 5π/4
Then
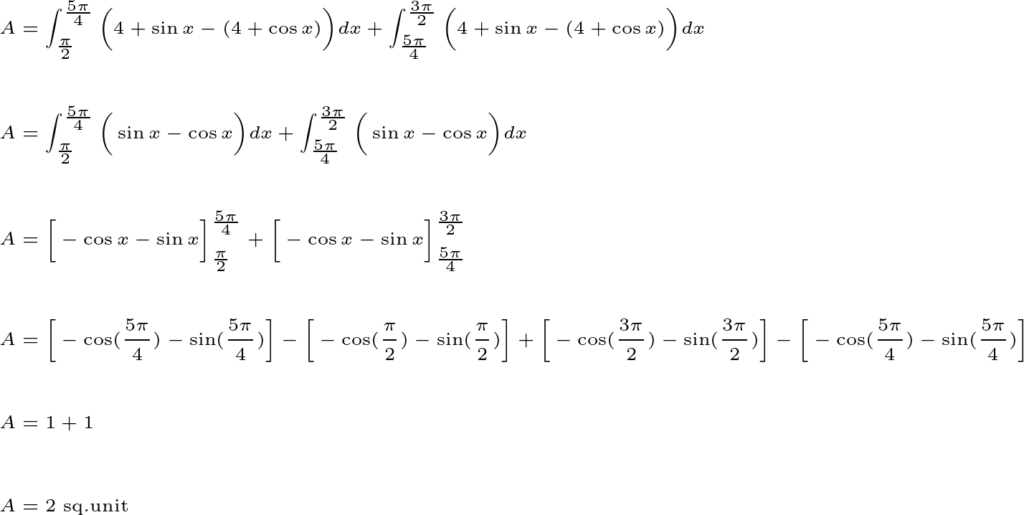
Area Enclosed by Two Curves: Curves Intersecting or Crossing at Two Points
If two curves cross or intersect, the area between them can be calculated by finding the difference of the definite integrals of the equations of the curves with limits as intersection points. By equating the curve equations, we can find the intersection points.
Steps for calculating the area between two curves (when curves intersect at two points)
- Determine the intersection points.
- Determine the area under both curves with limits as intersection points.
- calculate the difference between the areas under the curve
- To find the area between two curves, take the modulus value of the final result.
Here we are discussing the area enclosed by two curves x = 1 and y = x²
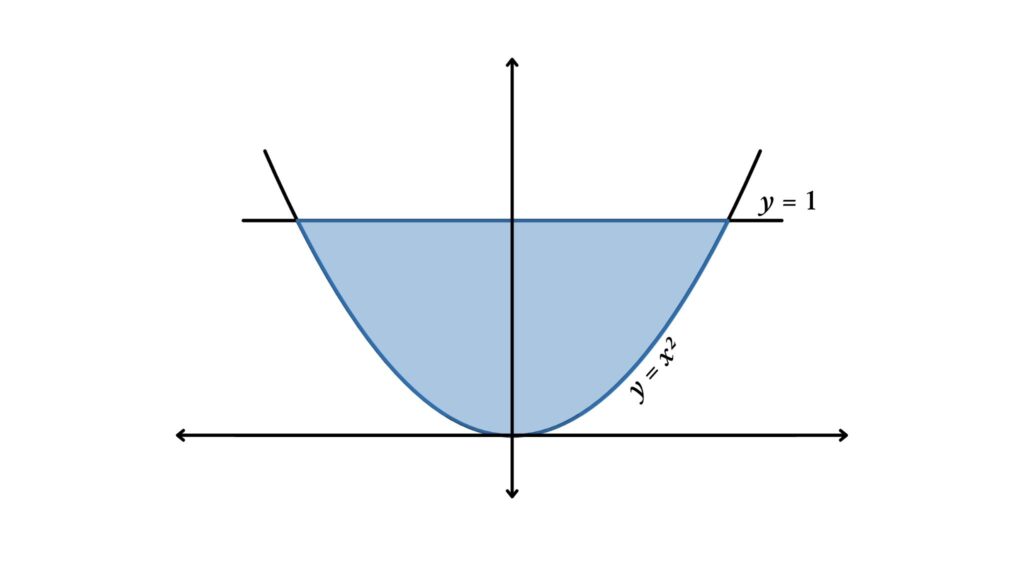
Here first we need to find the intersection points between the curves
y = x² = 1
x = ±1
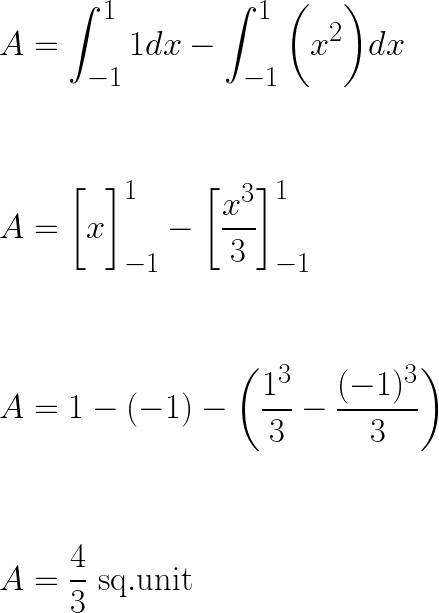
Area Between the Curve and the x-Axis When Curve Under x-Axis
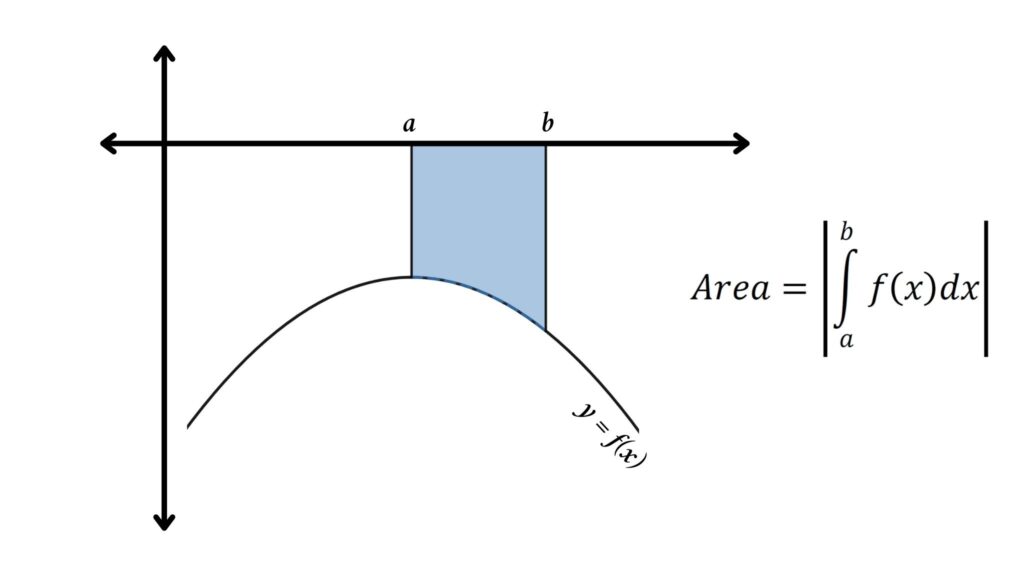
This is similar to the area under the curve. The only difference is that after calculating the integral, we will find the modulus of the result to determine the area between the curve and the x-axis.
From the figure area is
$$ | \int_{a}^{b} f(x) dx | $$
Area Between the Curve and the y-axis
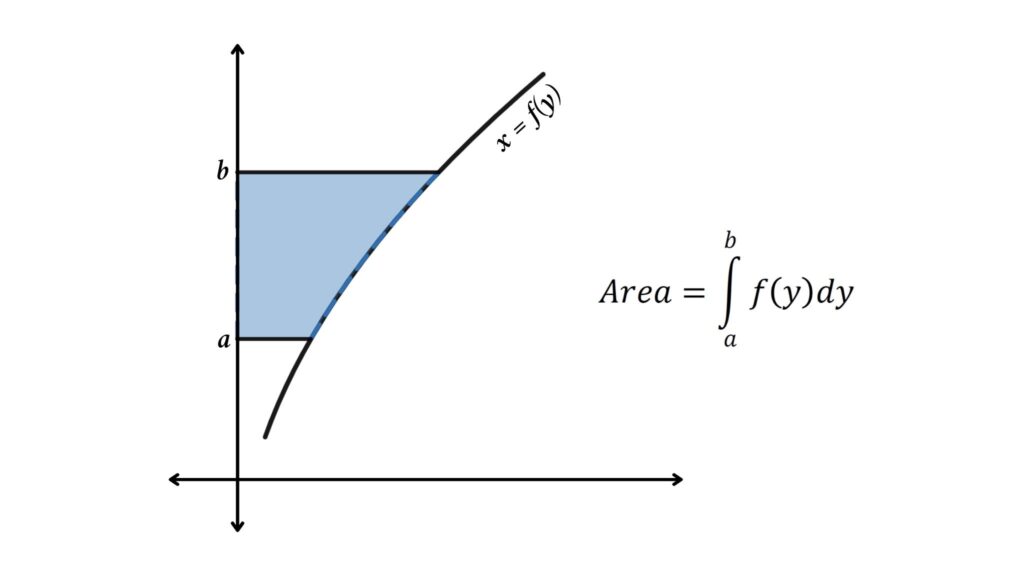
We saw that when the function is of the form y = f(x), we can easily find the area between the curve and the x-axis by integrating. However, if the function can be written in the form x = f(y), then we can calculate the area between the y-axis and the curve.
From the figure area between the curve and the x-axis is
$$ \int_{a}^{b} f(y) dy $$
