Geometry Math Problem: Find the area of the triangle
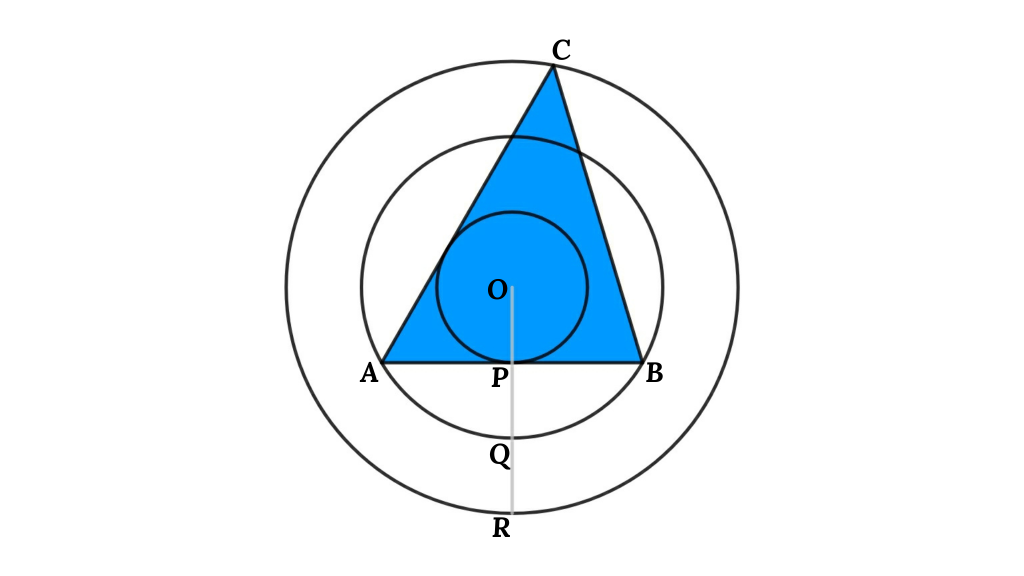
From the figure, We have three co-centric circles with center O, here OP = 1 cm, OQ = 1 cm, and OR = 3 cm. ABC is a triangle, and AB and AC are tangents of the smallest circle. Then find the area of the triangle Inside three circles (blue triangle).
Solution: Area of the triangle Inside three circles
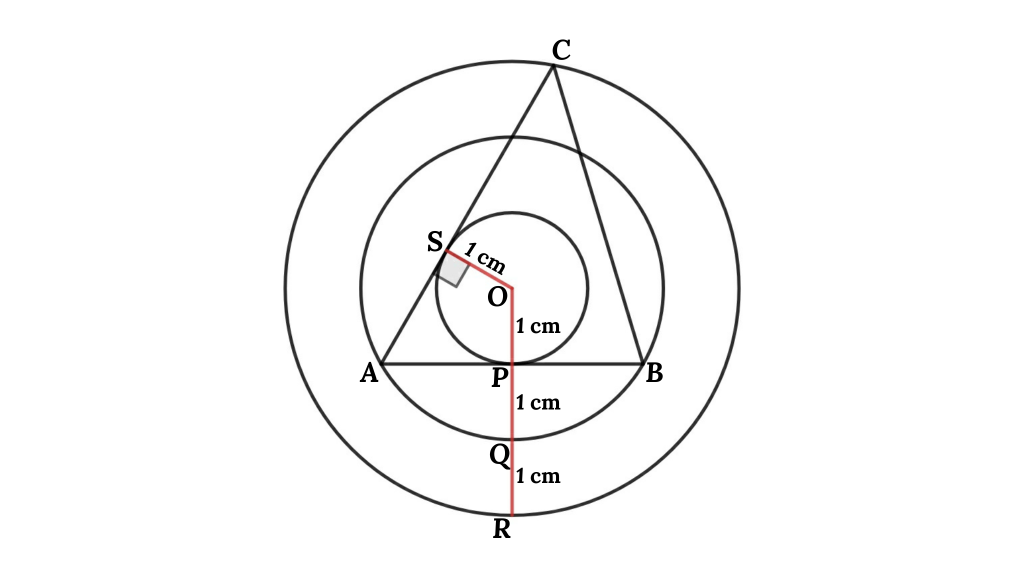
From this figure
P is the midpoint of chord AB because OP and AB are perpendicular to each other so, AP = BP
AS = AP (Tangent of the circle from Point A)
Now we can connect AE and AG so we can form two triangles
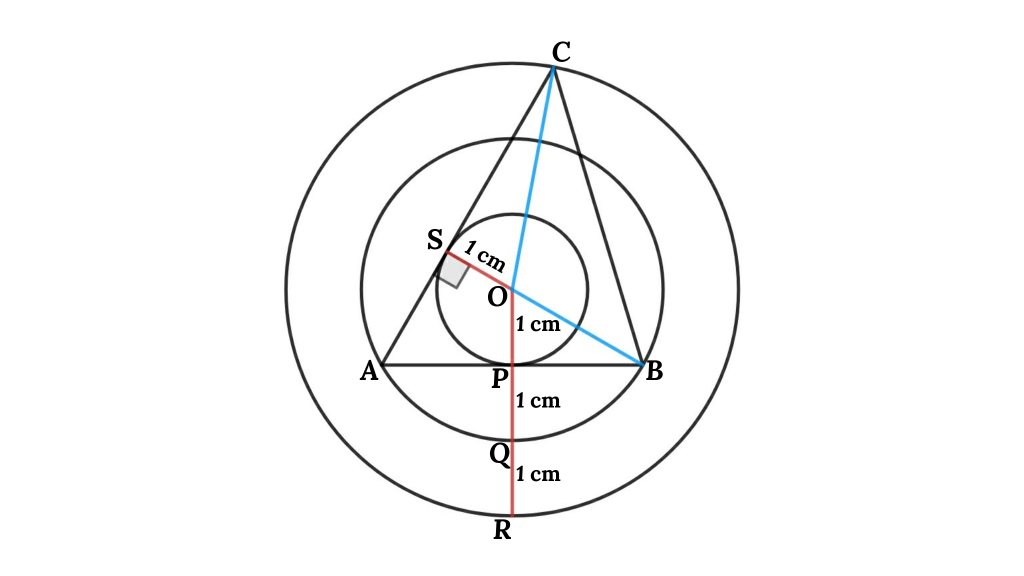
From triangle BOP
OB = 2 cm
OP = 1 cm
BP² = OB² – OP² = 2² – 1² = 4 – 1 = 3
⇒ BP = √3 cm
From triangle OCS
OC = 3 cm
OS = 1 cm
CS² = OC² – OS²
⇒ CS² = 3² – 1² = 9 – 1 = 8
so, CS = 2√2 cm
Then From ∆ABC
AB = AP + BP
⇒ AB = √3 +√3 = 2√3 cm
AC = AS + CS
⇒ AC = √3 + 2√2 cm
Connect B and T

Here we form a new triangle ABT with inner circle radius = 1 cm and outer circle radius = 2 cm, that is, Outer circle Radius = 2 × Inner circle Radius so we can understand ∆ ABT is an equilateral triangle
or, AB, BT, and AT are chords of circle ABT. These chords have the same distance from the centre so AB = BT = AT so we can say ∆ ABT is an equilateral triangle
That is ∠F = 60°
Then Area of Triangle = ½ × FE × FG × sin F = ½ × 2√3 × (√3 + 2√2) × (√3/2)
⇒ Area of Triangle = 3√2 + ½ × 3√3 cm²