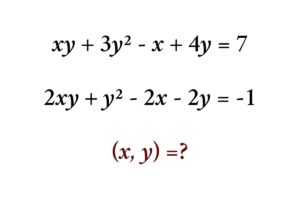Find the area of the rectangle formed by connecting the tangents of the circles

Three equal circles are touching each other. A rectangle is formed by connecting the tangents of these circles, Then find the area of the rectangle
Three circles have a 1 cm radius, These circles touch one another as shown in the figure. We can create a rectangle ABCD by connecting the tangents of the circles, what is the area of the rectangle ABCD?
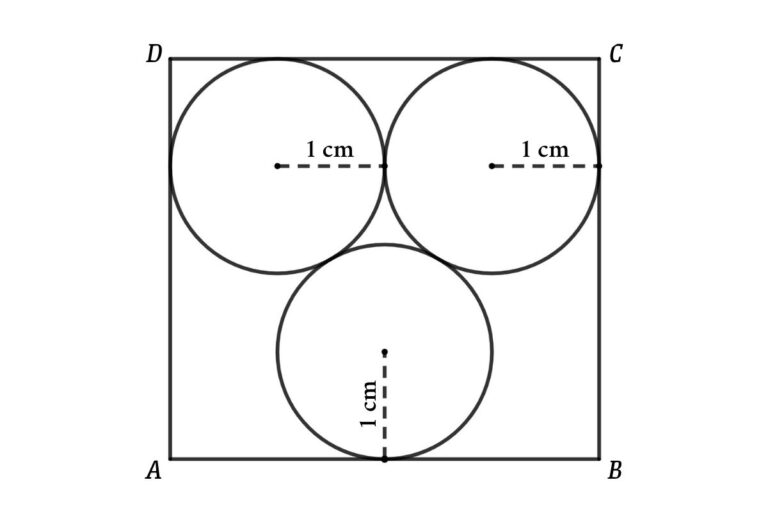
Solution
Draw PQ and RS as shown in the figure
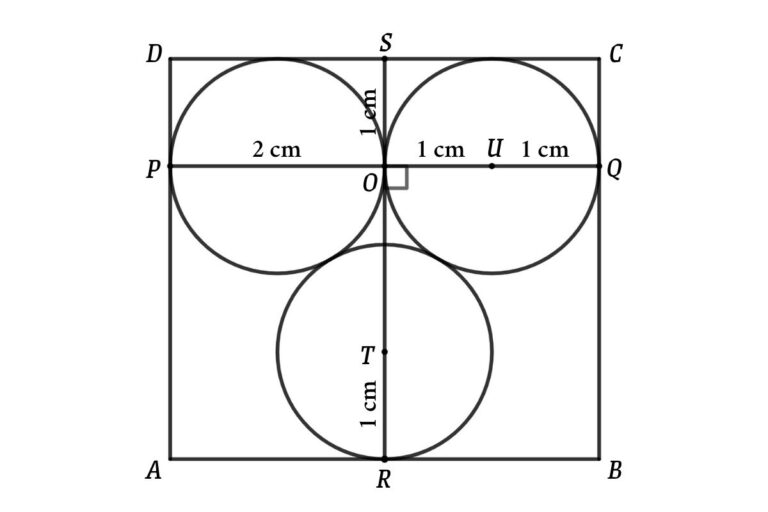
From figure
PO = 2 cm (Diameter of the circle)
TR = OU = UQ = 1 cm (Radius of the circle)
Connect UT, and then we get a right-angle triangle OUT
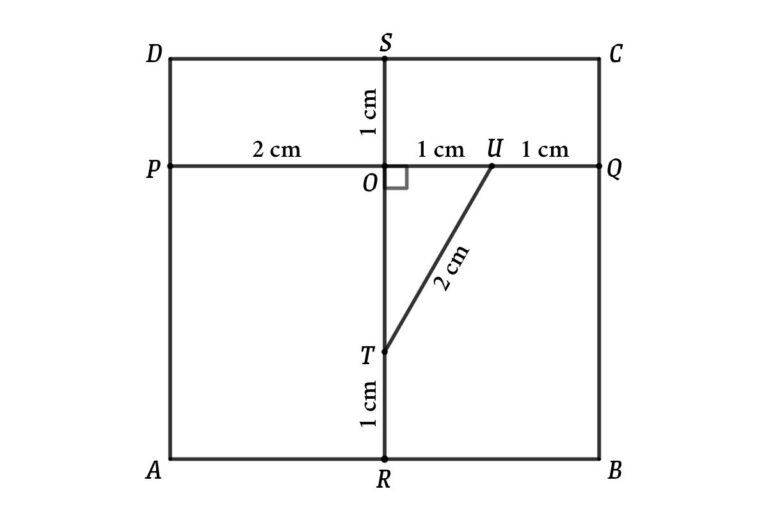
Apply Pythagorean theorem in triangle OUT
OT² = UT² – OU²
⇒ OT² = 2² – 1² = 4 – 1 = 3
⇒ OT = √3
PQ = PO + OU + UQ
⇒ PQ = 2 + 1 + 1 = 4 cm
SR = SO + OT + TR
⇒ SR = 1 + √3 + 1 = 2 + √3 cm
Area of rectangle = PQ × SR = 4(2 + √3) = 8 + 4√3 cm²