Geometry math problem: Find the area of the quadrilateral inside a square.
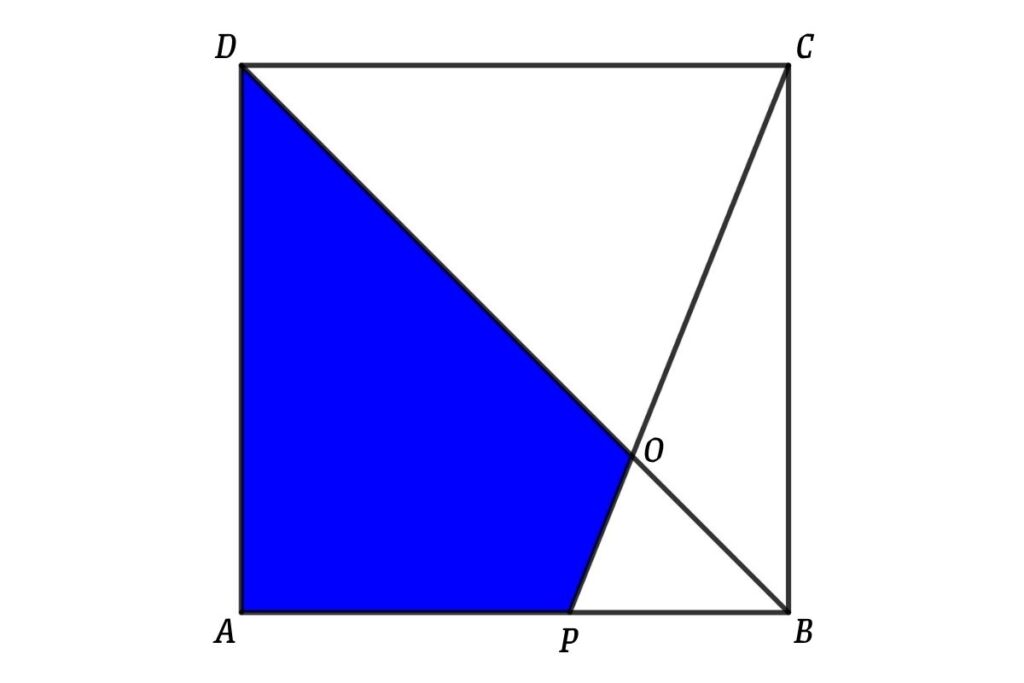
ABCD Is square also PA: PB = 3: 2, Connect BD and PC also measure OD = 25 cm Then find the area of quadrilateral APOD
Solution
Blue area = Area of ∆ABD – Area of ∆POB
Let’s consider the side of square = 5k, then
PA = 3k
PB = 2k
Also consider, OB = x
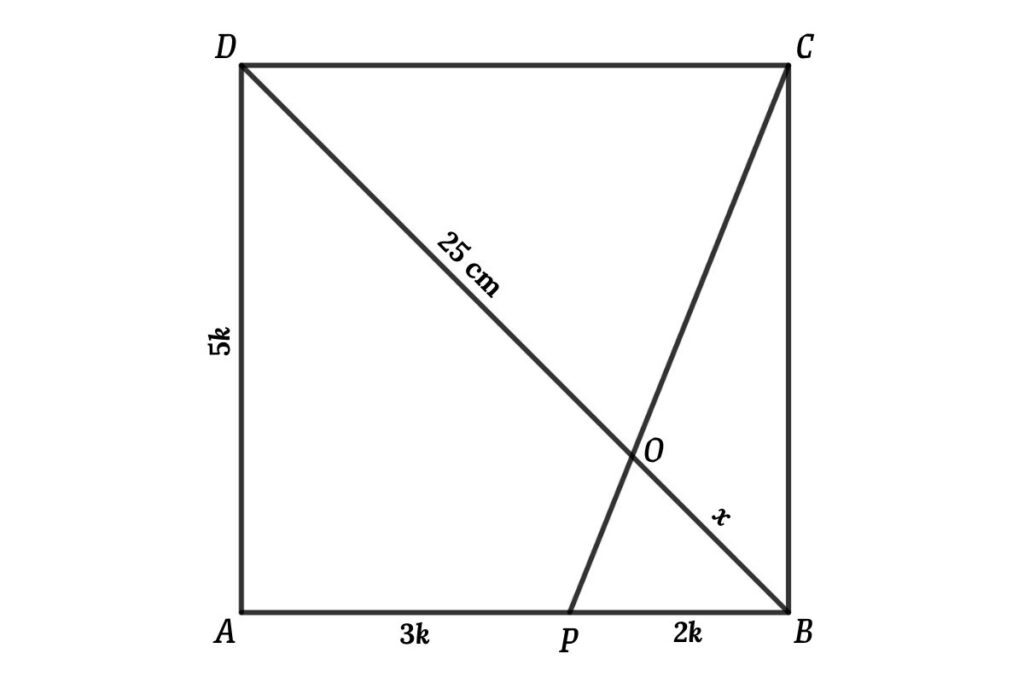
Consider ∆OCD and ∆OPB
We know CD and PA are parallel lines
Then
CD/PB = 25/x
(5k)/(2k) = 25/x = 5/2
So, x = 50/5 = 10 cm
Also BD = 25 + 10 = 35 cm
Apply Pythagorean theorem in ∆ABD
Then BD = 5k√2 = 35
k = 7/√2 cm
Now draw heights of the triangle
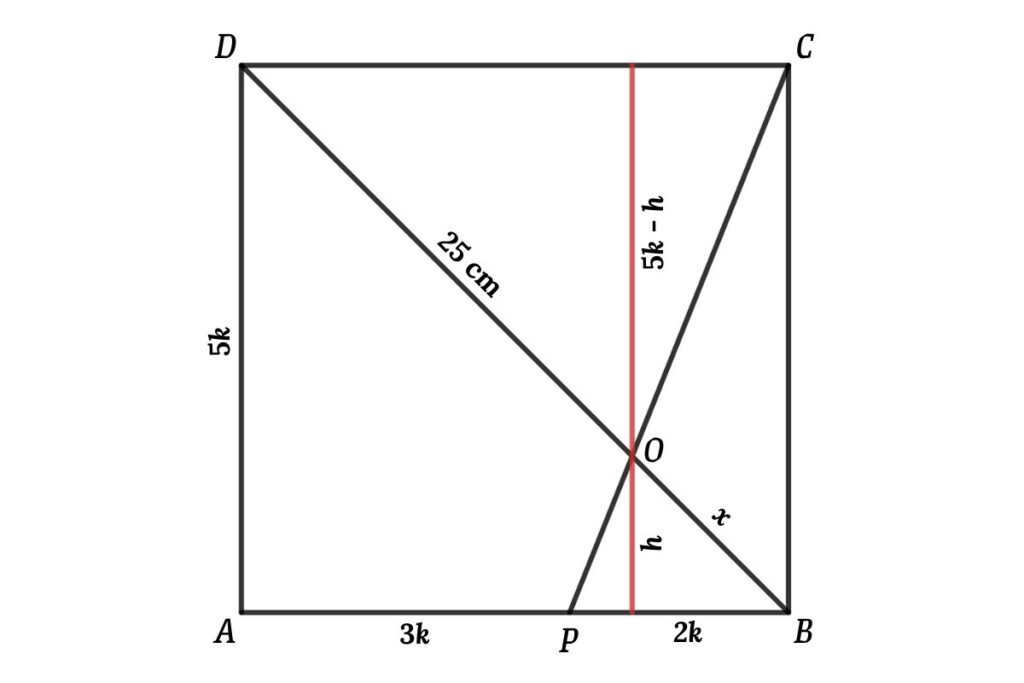
From ∆ODC and ∆POB
(5k – h)/h = 5/2
h = 5√2 cm
So Blue area = ½ (5k)² – ½ 2kh
= ½ 25 (7/√2)² – 7/√2 × 5√2
= 1085 / 4 cm²
Area of quadrilateral = 271.25 cm²