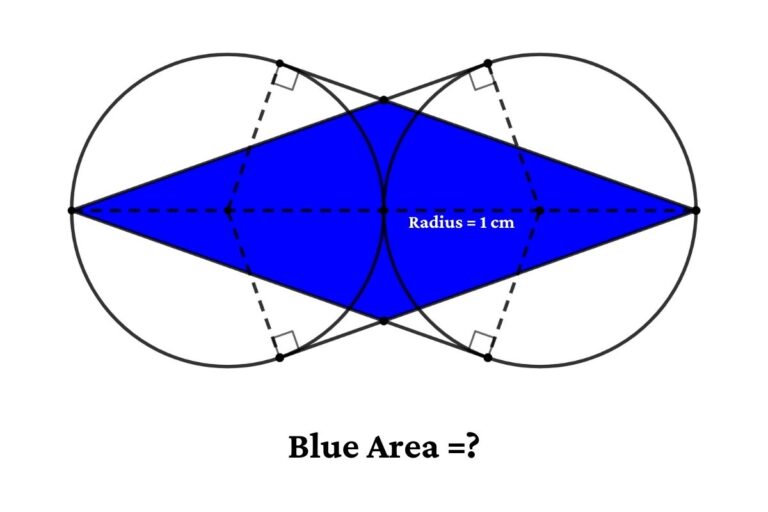
Geometry math problem – find the area of the “parallelogram” between two circles, the sides of the parallelogram formed by connecting the tangents of the circle. tangents are starts from two ends of a line, which is formed by diagonals of the two circles
How to find the area of the parallelogram between two circles?
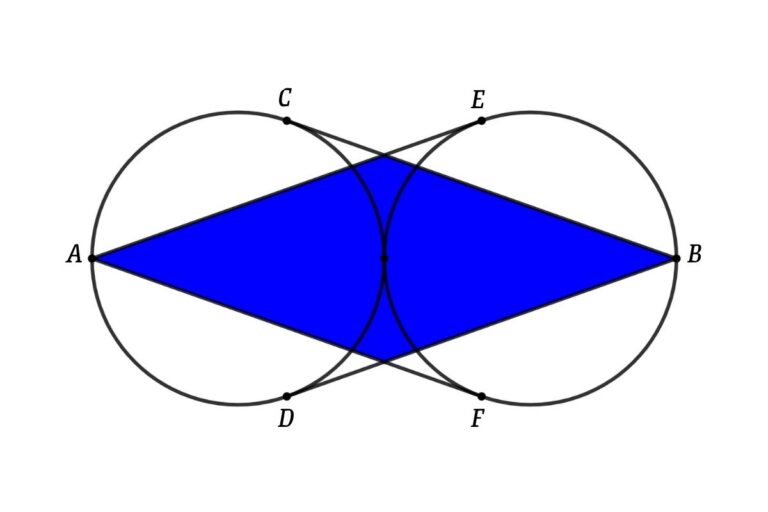
From the figure, BC, BD, AE, and AF are tangents, If the radius of two circles is 1 cm find the area of the blue parallelogram
Solution
We can start from the figure
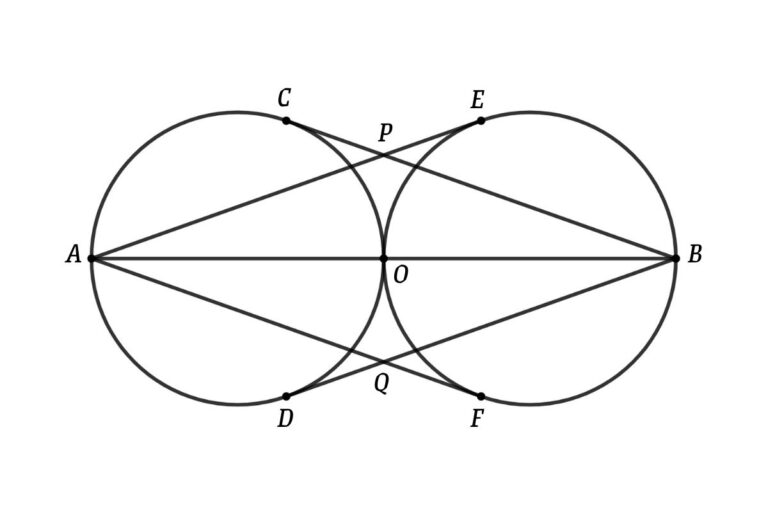
From the figure, the Area of the triangle PAB = Area of the triangle QAB
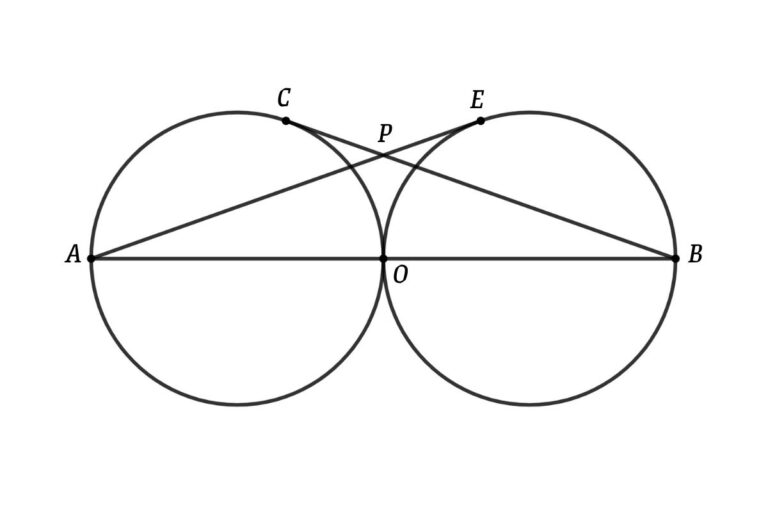
Connect PO and C with the center of the 1st circle
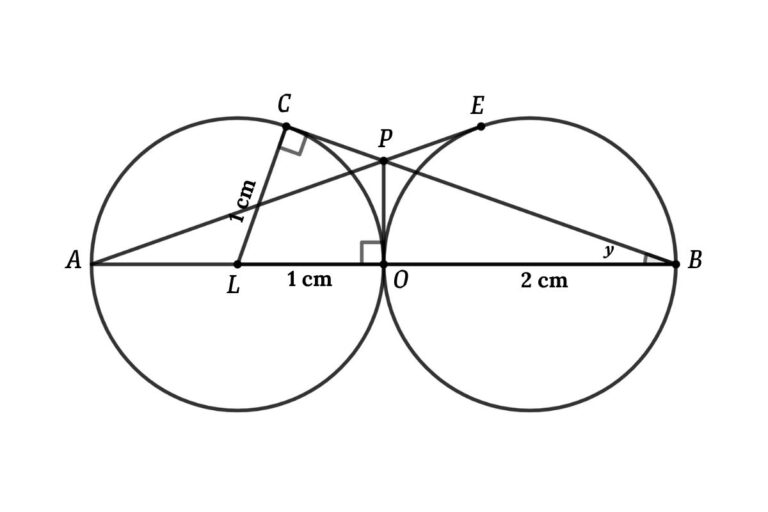
From triangle BCL
sin y = CL/BL
⇒ sin y = 1/3
⇒ tan y = 1/(2√2)
From triangle BOP
tan y = PO/BO
⇒ tan y = PO/2
⇒ PO/2 = 1/(2√2)
So, PO = 1/√2
Area of the triangle PAB = ½ × AB × PO
⇒ Area of the triangle PAB = ½ × 4 × (1/√2)
⇒ Area of the triangle PAB = √2 cm²
So, the Area of the parallelogram = 2 × √2
⇒ Area = 2√2 cm²