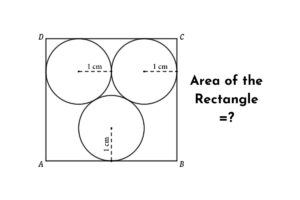
Find the Relation between the Area of a Circle and the Semicircle Inside a Square
From the figure, ABCD is a square and CT is the tangent of the semicircle and circle. Then find the Relation between the area of the semicircle and the area of the circle inside the square.
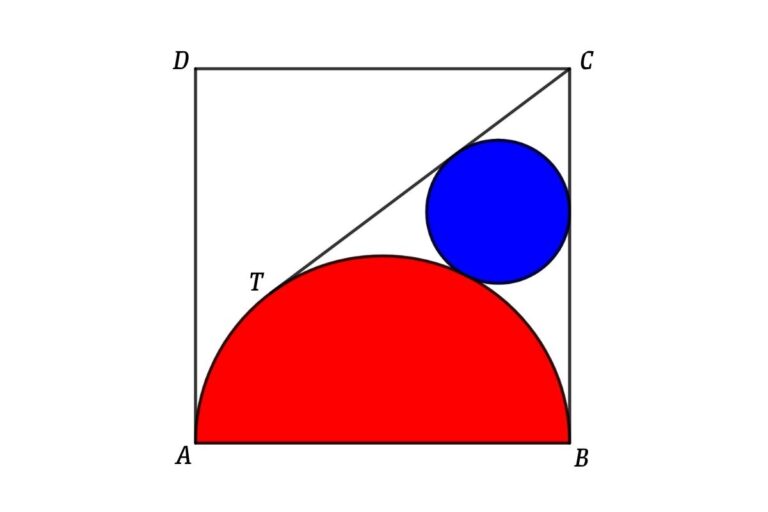
Solution
Connect C and the center of the semicircle

Let’s assume the radius of the semicircle is R and the radius of the circle is r, then
Area of red semicircle = πR²/2
Area of blue circle = πr²
Now, the area of the blue circle/area of the red semicircle = (πr²)/(πR²/2)
⇒ Area of blue circle/area of red semicircle = 2r²/R²
Apply Pythagoras’ theorem in the triangle OBC
OC² = OB² + BC²
⇒ OC² = R² + (2R)²
⇒ OC² = R² + 4R² = 5R²
Thus, OC = R√5
From the figure triangle OBC and triangle PQC are similar, so
OB/PR = OC/PC
⇒ R/r = (R√5)/(R√5 – (R + r))
⇒ R(R√5 – (R + r)) = (R√5)r
so, R√5 – (R + r) = r√5
⇒ R(√5 – 1) = r(√5 +1)
⇒ r/R = (3 – √5)/2
Square both sides, then
r²/R² = (3 – √5)² / 4 = (14 – 6√5) / 4
⇒ r²/R² = (7 – 3√5) / 2
⇒ 2r²/R² = 7 – 3√5
Area of blue circle/area of red semicircle = 7 – 3√5