Find the Area between Two Semicircles

Find the area between two semicircles, when a small semicircle is inscribed in a larger semicircle as shown in the figure. (find the area of blue shaded region). The diameter of the smaller semicircle is the chord of the larger semicircle

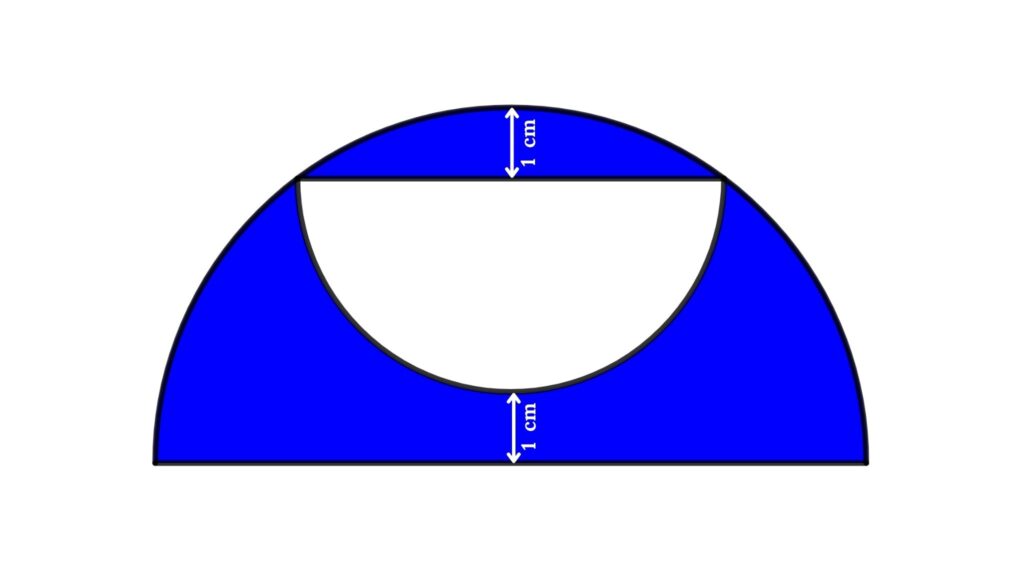
Solution

Area of the blue region = Area of the larger semicircle − Area of the smaller semicircle

We can redraw the figure as shown below

Here OA = OB

∠BOQ = 90°

Let the radius of the larger semicircle = r, then

OR = r − 2 → OR is the radius of the smaller semicircle

OR = OA = OB = r − 2 {radius of the semicircle}

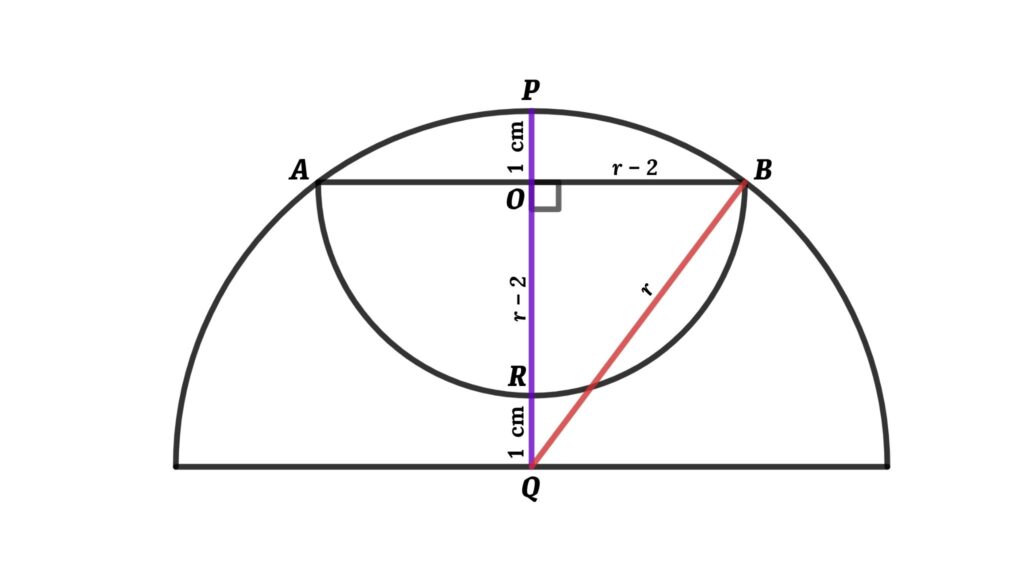
Apply Pythagorean theorem in triangle BOQ

OQ² + OB² = BQ²

⇒ (r − 1)² + (r − 2)² = r²

⇒ r² − 2r +1 + r² − 4r + 4 = r²

Now, r² − 6r + 5 = 0

Factorise r² − 6r + 5

Then, r² − 6r + 5 = r² − r − 5r + 5 = r(r − 1) − 5(r − 1) = (r − 1)(r − 5) = 0

so r = 1 cm or r = 5 cm

The radius of the larger semicircle is greater than 2 cm so r = 5 cm and r − 2 = 3 cm

That is the radius of the larger semicircle = 5 cm and the radius of the smaller semicircle = 3 cm

Now we can find the area of semicircles

Area of the larger semicircle = ½ × π × 5² = 25π/2 cm²

Area of the smaller semicircle = ½ × π × 3² = 9π/2 cm²

The difference between areas of semicircles gives the blue area, so

Blue area = 25π/2 − 9π/2 = 16π/2

⇒ Blue area = 8π cm²