How to Solve a System of Linear Equations

Vector Form of System of Linear Equations

An equation involving a linear combination of vectors and possible unknown coefficients is known as a vector equation

Matrix Form of System of Linear Equations

Three matrices can use to represent a system of linear equations. those are a coefficient matrix, a variable matrix, and a constant matrix.

Dependent System: Leniar Equations Have Infinitely Many Solutions

When we solve a system of equations,

1. The number of unknowns is less than the set of equations.
2. We get like 0 = 0 or similar forms.
3. Unsolvable linear equations

For example, if  x + y + z = 9 and x + 2y + 2z = 16 are system of equations with three variables but only having two set of equation. When solving this system, we can find that this equation set has an infinite number of solutions, that is 

To solve this system let’s start by multiplying   x + y + z = 9 by 2, the equation becomes 

2x + 2y + 2z = 18

In the next step we are subtracting  x + 2y + 2z = 16  from  2x + 2y + 2z = 18 then we get  x = 2

When we replace x = 2 in the system, we get two new equations: y + z = 7 and 2y + 2z = 14. When we look at these equations, we can see that both equations are the same, but the second equation is a multiple of the first.

So if we do elimination here, we get 0 = 0 form, which means y and z have infinite solutions but satisfy the equation y + z = 7 or z = 7 – y, that is when y = 1 then z = 6 if y = 2 then z = 5, and so on y can have any real value so the solution set is infinite but the value of x is always 2, or we can write the solution set as  (x, y, z) = (2, 1, 6), (2, 2, 5), (2, 3, 4) and so on

Independent System: Leniar Equations Have a Unique Solution

A system of linear equations has a unique solution then we can also say that each variable has one solution. The number of equations must equal the number of unknowns if a system has a unique solution. Even also a unique solution is not guaranteed for the system of equations.  If it has a unique solution, that will satisfy all equations in the system.

For example,

x + y + z = 9……………..eq(1)

x + 2y + 2z = 16…………..eq(2)

2y + z = 10………….……eq(3)

This set of equations has three equations and variables. We can use the substitution method to solve this system of equations, after solving this system we get (x, y, z) = (2, 3, 4) as the solution.

Inconsistent System: Leniar Equations Have no Solution

If the ratio of the unknown variables’ coefficients is equal and which is not equal to the ratio of the constants, then the equation system has no solutions. 

We can also say this mathematically 

Let us consider two linear equations in x and y

a₁x + b₁y = c₁

a₂x + b₂y = c₂

If this system has no solution then   a₁/a₂ =  b₁/ b₂ ≠ c₁/c₂

For example, consider the system of linear equations  4x + 6y = 3  and  10x + 15y = 6

Now the ratio of the coefficient is   4/10 and  6/15 which is equal to 2/5 

Now the ratio of constants is 3/6 which is equal to 1/2 

2/5 ≠ 1/2   so the system has no solution

Using Elimination

1. Pick two equations and make one of the unknown variables’ coefficients equal by multiplying or division
2. Add or subtract the equations and eliminate unknowns with the same coefficients
3. Steps 1 and 2 are repeated until the system is reduced to a single linear equation.
4. Solve this equation and then back-substitute until you find the complete solution.

For example, consider a linear equation system with three variables and equations. Solve the system  2x + y + z = 7, 3x + 2y + 3z = 16, and x + 3y + 2z = 13

Let’s start with Naming the equation

2x + y + z = 7……………………………eq(1)

3x + 2y + 3z = 16…………………………eq(2)

x + 3y + 2z = 13……………………..……eq(3)

We will eliminate unknowns one by one. Here we eliminate z first. 

Consider eq(1) and eq(3)

Let’s start with multiply eq(1) by 2,  then the coefficients of z in eq(1) and eq(3) become equal.

4x + 2y + 2z = 14………….…………………eq(4)

We can subtract eq(3) from eq(4) then we can remove z.

So, 3x – y = 1……………………………….…eq(5)

Now consider equations eq(1) and eq(2)

multiply equation 1 by 3,  then the coefficients of z in equations 1 and 2 become equal.

6x + 3y + 3z = 21………….…………………eq(6)

We can subtract eq(2) from eq(6) then we can remove z.

(6x + 3y+ 3z) – (3x + 2y + 3z) = 21 – 16

So, 3x + y = 5…………………………………eq(7)

Here we got a pair of equations in x and y (equations 5 and 7)

Now we can eliminate y  from the pair of equations by adding equations 5 and 7

(3x – y)+(3x + y) = 1 + 5

Then, 6x = 6

x = 1

Now substitute the value x in eq(7) then we get y = 2. To find the value of z just substitute x and y in any three of the equation in the system of linear equations so we get z = 3

So the solution is x = 1, y = 2, and z = 3

Using Graphs

We can solve a  two-variable linear system of equations very easily by plotting the graphs and the coordinates of the intersecting point will give you the solution. 

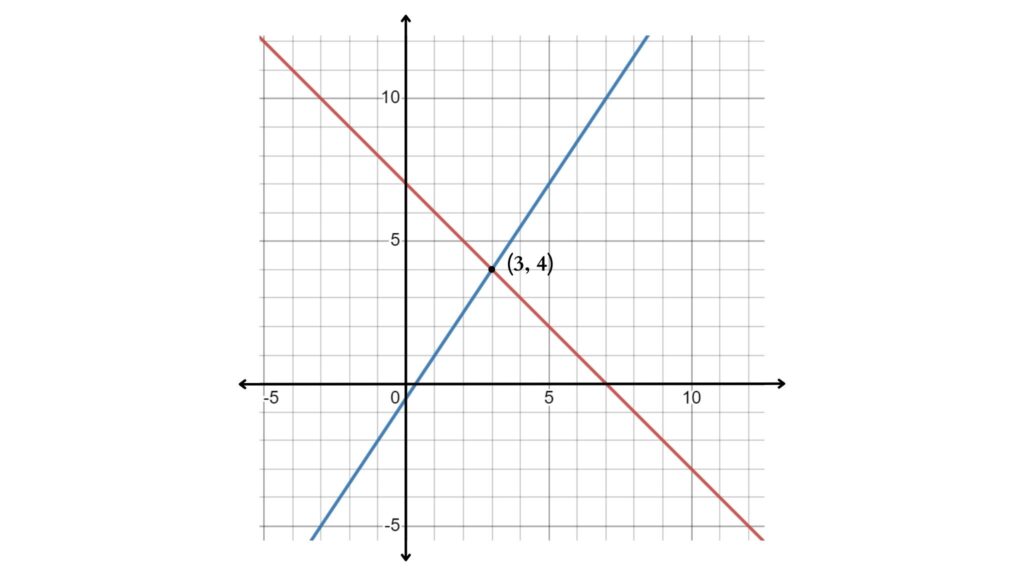
The figure shows the graph of 3x – 2y = 1  and  x + y = 7 which crossing intersect at (3, 4), so the solution is  x = 3  and y = 4

Using Matrices

We saw how matrices can represent a system of linear equations. Simple systems can be solved quickly and easily through substitution, elimination, or graphing. But larger systems are handled with matrix techniques.

If |A| ≠ 0 then the system is consistent and has a unique solution then  X = A⁻¹B will give the solution where A is the coefficient matrix, X is the variable matrix, and B is the constant matrix. A⁻¹ is the inverse of the matrix 

For example, consider the system 2x + y + z = 7, 3x + 2y + 3z = 16, and x + 3y + 2z = 13, Here we get matrices A, B, and X as follows

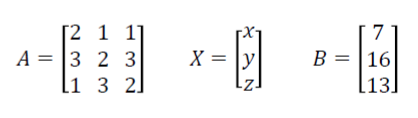
We know  X = A⁻¹B, so we need to find A⁻¹

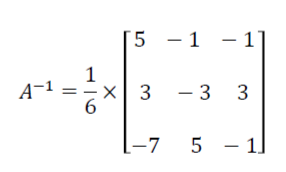
Now we get

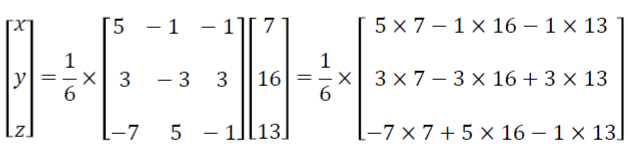
Simplify this, then

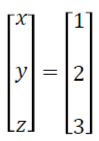
So x = 1, y = 2 and z = 3