Table of Contents
ToggleWhat is a quadratic equation?
If an equation can be expressed in the standard form of a quadratic equation ax2 + bx + c = 0, then it is said to be a quadratic equation. Due to the degree of the polynomial being two, it is also known as a second-degree equation. where a ≠ 0, x is the variable, and a, b, and c are coefficients.
If a = 0 then the standard equation becomes bx + c = 0, which is a linear equation with the solution x = -c/b.
A second-degree equation can also be represented in a factored form, such as (x-m) (x-n) = 0, where m & n roots of quadratic equation.
Quadratic Equation Examples
x2 + 2x + 1 = 0
x2 – 2x + 6 = 0
2x2 + 5x + 5 = 0
x2 + 2x = 0
Graphical Representation of Quadratic Equations
We can plot the graph of quadratic equations symbolically because it is a polynomial with only one variable. In this case, x is a variable in the equation, and y is the quadratic equation. or we can simply say y = ax2 + bx + c.
The quadratic equation’s graph is always a parabola. It has real solutions if it crosses or touches the x-axis; otherwise, it only has imaginary roots.
The roots of the sample graph shown here are real. Otherwise, the graph should be above the x-axis.

How to Solve a Quadratic Equation?
Solving quadratic equations means evaluating the values of the variable that satisfy the equation, these values are known as their roots or solutions. A quadratic equation has a maximum of two roots because its degree is two.
A second-degree equation has one root if b2 – 4ac = 0, and two roots if b2 – 4ac is not equal to 0. Likewise, if b2 – 4ac > 0 then it has only real roots; otherwise, it has only complicated roots.
Method 1
Solving the Quadratic Equation by Completing the Square
Quadratic equations can be expressed as the square of linear equations, so we can solve them simply by taking the square roots. when taking the square roots we should aware of taking all possible square roots (Positive and negative)
Steps involved in solving a quadratic equation by completing the square
- Change the form of the equation to ax2 + bx = -c
- Complete the square by adding the term to both sides.
- Apply the square root property to the resulting equation to solve it.

Let’s start with general equation ax2 + bx + c = 0
We can write ax2 + bx = -c. Divided both sides with a then,
x2 + bx/a = -c/a, now add square of the half of the coefficient of x, that is (b/2a)2
x2 + bx/a + (b/2a)2 = -c + (b/2a)2.
We know the identity for (a + b)2 = a2 + 2ab + b2 {or, binomial expansion of (a + b)2}
so, (x + b/2a)2 = -c + (b/2a)2. Let u = b/2a and v2 = -c + (b/2a)2 then
(x + u)2 = v2
take square roots
x + u = ±v
⇒ x = -u ±v
Example Problem: solve the equation x²+5x+6=0 by completing the square
x2 + 5x = -6
⇒ x2 + 5x + (5/2)2= -6 + (5/2)2
then, (x + 5/2)2= -6 + 25/4 = ¼
x + 5/2 = ±½
so, x = ±½ – 5/2
⇒ x = -2 and x = -3
Method 2
Solving Quadratic Equation by Factorization
In this method, we represent the quadratic equation as the product of their factors. That is we are going to represent them in the form (x-m)(x-n) where m and n are the roots of the equation
Or ax2 + bx + c = (x-m)(x-n) = x2 – (m+n)x + mn = 0, so we get -(m+n) = b and c = mn
Now we need to find two numbers (m & n) that satisfy the equation for a and b so these two numbers are the solutions.
Steps involved in solving by Factorization
- Factorize the non-zero side.
- Equate each factor to zero (A product of factors is zero if and only if one or more factors are zero)
- Solve each resulting equation.
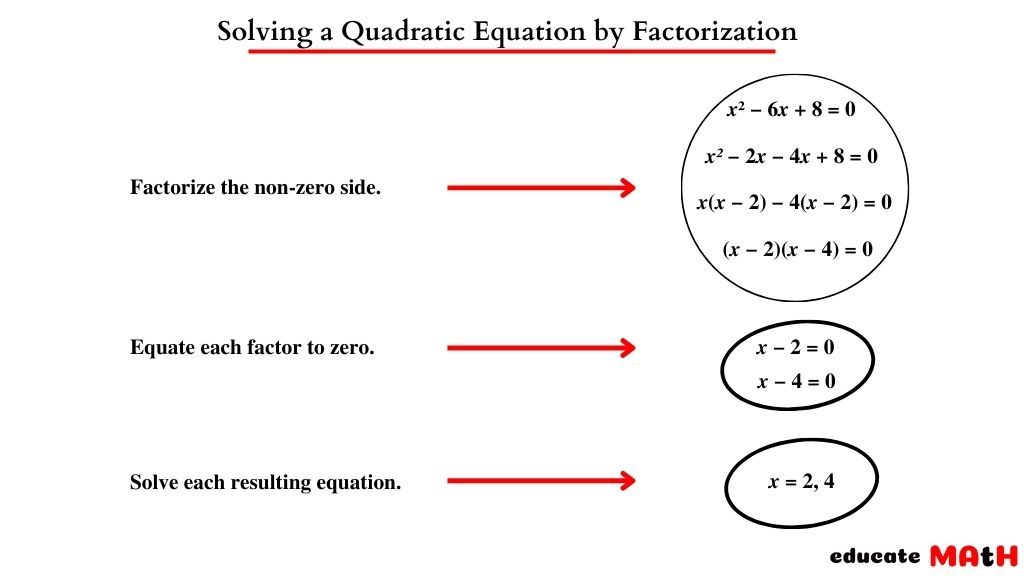
Example Problem: Solve the equation x²+5x+6=0 by factorization
From above equation we get b = -(m+n) = 5 and c = 6 = mn
Here we can guess m = -2 and n = -3 so solution of the equation are -2 & -3
Method 3
Solving with the Quadratic Formula
A quadratic formula gives the solution of the quadratic equations when we plug in the values of coefficients in the equation
We can derive x from the equation that is

Proof of Quadratic formula
ax2 + bx + c = 0
⇒ ax2 + bx = – c
so, x2 + bx/a = – c/a
⇒ x2 + bx/a + (b/2a)2 = – c/a+ (b/2a)2
thus, (x + b/2a)2 = – 4ac/4a2+ b2/4a2 = (b2 – 4ac)/4a2
x + b/2a = ±√(b2 – 4ac)/2a
x = (-b ±√(b2 – 4ac))/2a
Example problem: Solve the equation x2+5x+6=0 using quadratic formula
x = (-5 ±√(52 – 4×1×6))/2×1
⇒ x = (-5 ±√(25 – 24))/2
⇒ x = (-5 ± 1)/2
then, x = -2 & x = -3
Method 4
Graphical Solution of Quadratic Equation
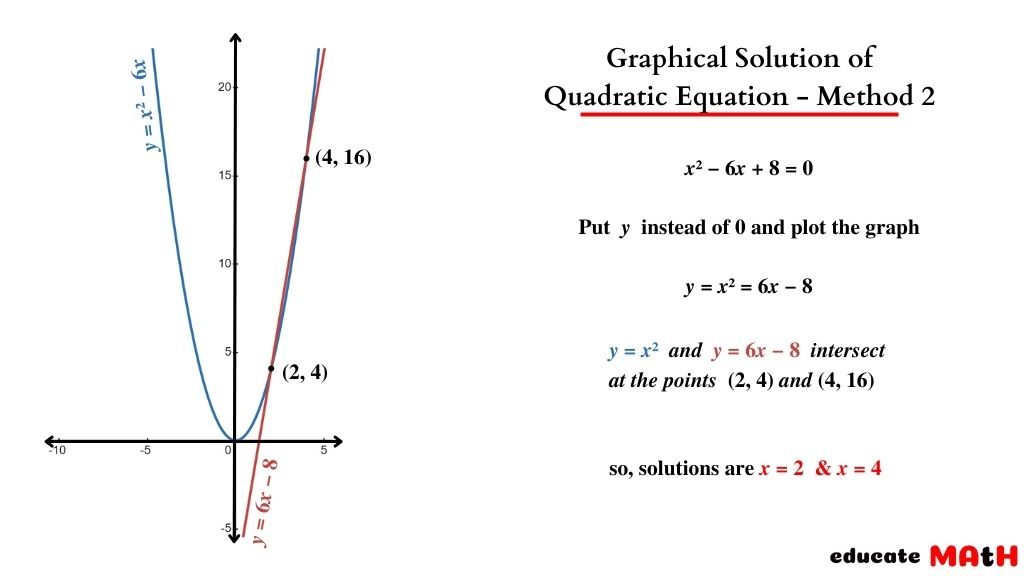
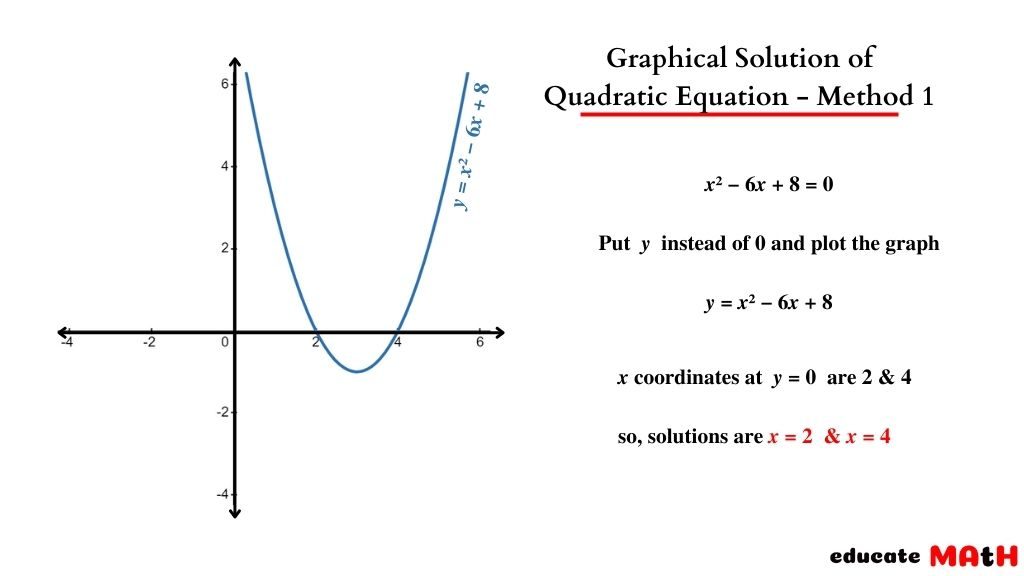
There are two ways to solve a quadratic equation graphically. Both approaches are simple and comparable, in the first approach, we plot a single graph, and the x-intercepts represent the solution to the equation. But in the second method, two simple graphs are plotted, and the x coordinate of intersecting points determines the equation’s solution.
In the first method, graphing a quadratic equation against the y-axis. specifically, the graph of y = ax2 + bx + c, and the x coordinates at y = 0 are the solutions to the equation.
In the second method, we divide the quadratic equation into two simple graphs against the y-axis. The graphs of y = ax2 (parabola) and y = bx + c (line), followed by the x coordinates of intersection points, will give the solutions.