Application of Integration: Definite integral math problem
The figure shows two parabolas and a circle. The circle passes through the parabolas’ vertex and the origin’s center. If parabolas are y = x²/4 – 2 and y = –x²/4 + 2 then find the area between the circle and the parabola using integration
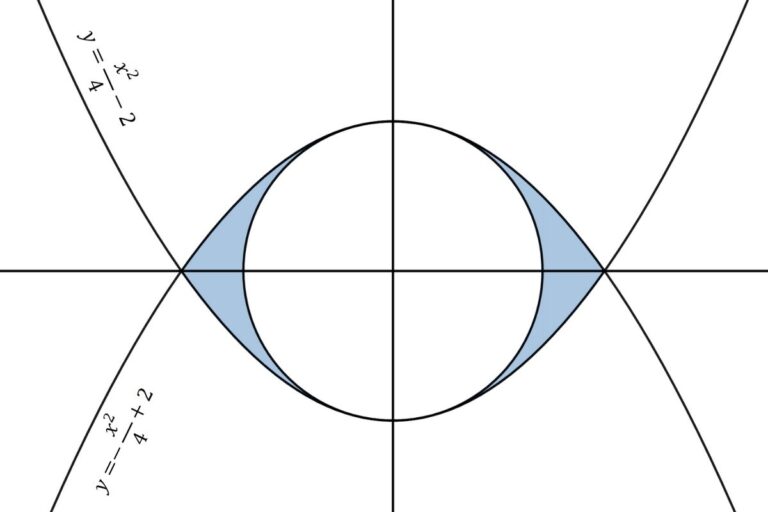
The area between the circle and the parabola
If we need to find the area using integration, then we need the intersection points of the curves
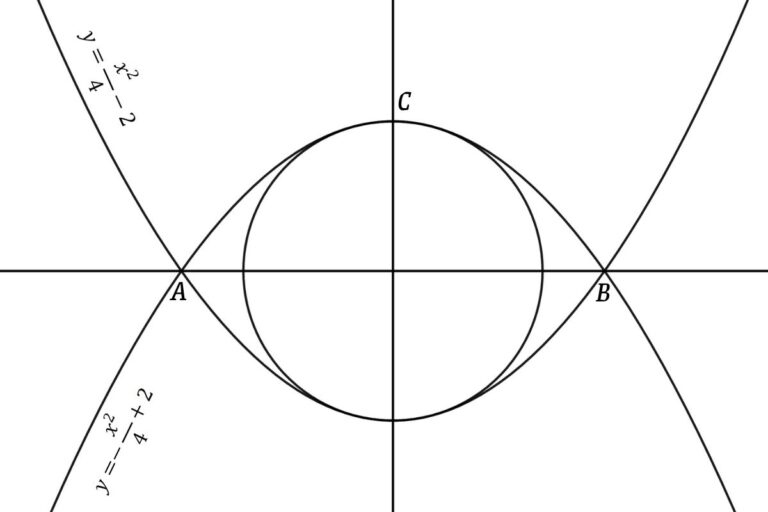
From figure
to find the intersecting points of the parabolas we can equate y = x²/4 – 2 and y = –x²/4 + 2 (we can also equate with the x-axis)
x²/4 – 2 = –x²/4 + 2
⇒ x²/2 = 4
⇒ x² = 8
⇒ x = 2√2
then, y = 0
So intersecting points are (2√2, 0), (-2√2, 0)
that is A = (-2√2, 0) and B = (2√2, 0)
Point C is the intersecting of the parabola and circle (C also belongs to the y-axis)
y = –x²/4 + 2
⇒ y = 0 + 2
that is C = (0, 2) which means the radius of the circle = 2 cm
so the equation of the circle is x² + y² = 4

The above figure is symmetrical through the x-axis so we can find the area between the circle and parabola is twice the upper shaded area
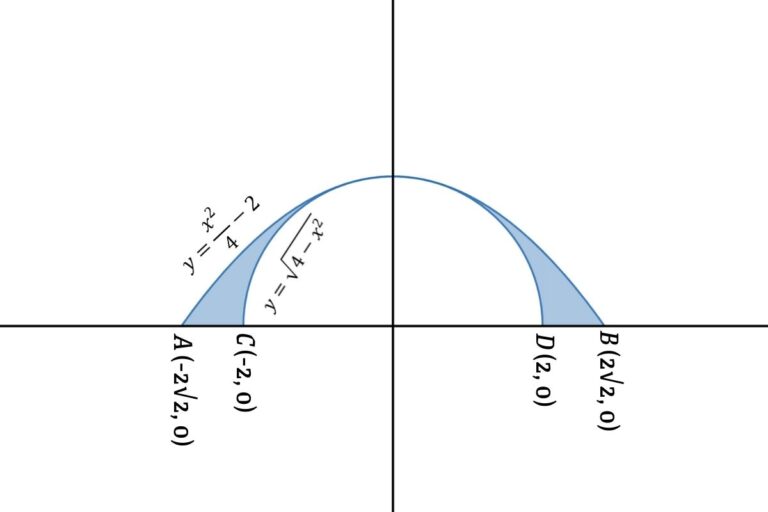
Now we can find the area of the parabola and the area of the semicircle separately and the difference between them is the upper shaded area
The area of the parabola

From the figure, the area of the parabola is

So we got the area of the parabola as (16√2)/3 unit² (Area is always positive)
The area of the semicircle


So the area of the semicircle is 2π unit²
The area of the upper shaded region is (16√2)/3 – 2π unit²
thus the area between the parabola and circle is (32√2)/3 – 4π unit²