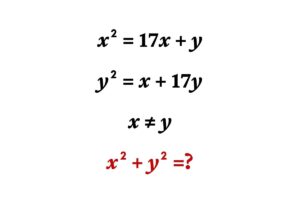Find the area of the triangle formed by connecting opposite corners of the square and the center of the circle.
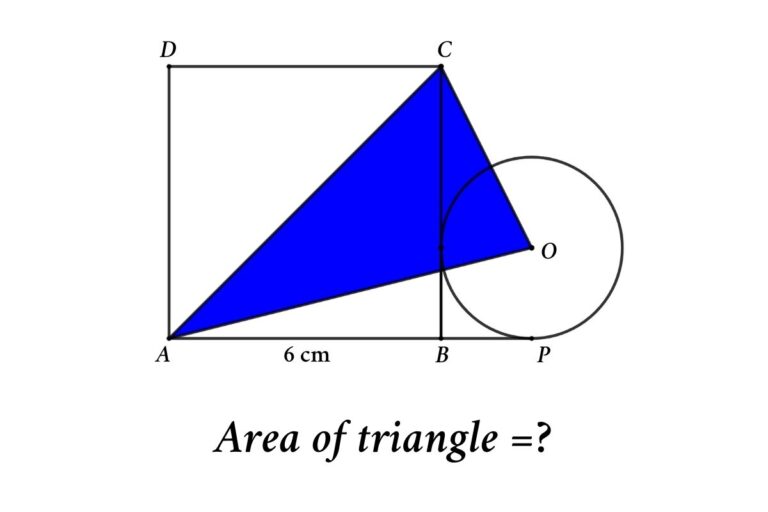
Find the area of the triangle
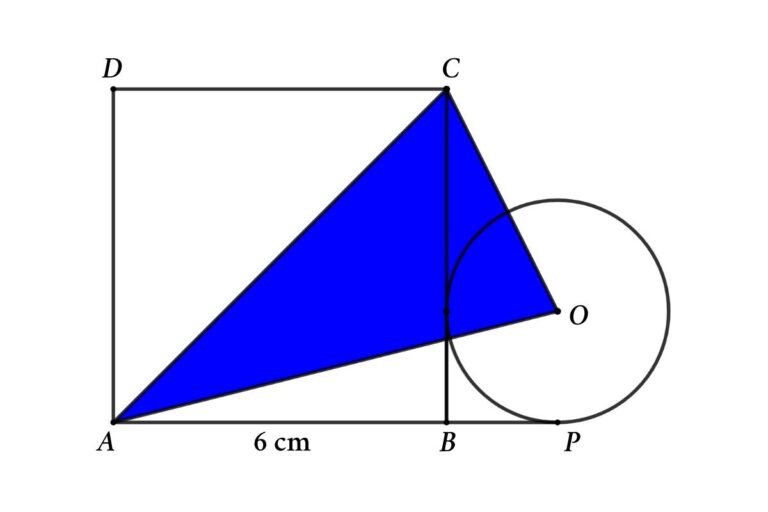
From the figure, ABCD is a square with sides 6 cm in length. AP and BC are tangents of the circle. Connecting two corners of the square and the center of the circle to form a triangle, then find the area of the triangle
Solution
Extent PO and DC then we get a rectangle APSD

Let’s assume the radius of the circle is r, then ST = 6 – 2r
Consider rectangle APSD

From the figure, the Area of the blue triangle = Area of the rectangle APSD – Area of the red triangle – Area of the yellow triangle – Area of the green triangle
1. Area of rectangle APSD = AP × AD = (6 + r) × 6 = 36 + 6r cm²
2. Area of the red triangle = ½ × DA × DC = ½ × 6 × 6 = 18 cm²
3. Area of the yellow triangle = ½ × SC × SO = ½ × r × (6 – r) = 3r – r²/2 cm²
4. Area of the green triangle = ½ × PO × PA = ½ × r × (6 + r) = 3r + r²/2 cm²
We know the area of the blue triangle = Area of the rectangle APSD – Area of the red triangle – Area of the yellow triangle – Area of the green triangle
⇒ Area of blue triangle = 36 + 6r – 18 – (3r – r²/2) – (3r + r²/2)
⇒ Area of blue triangle = 36 + 6r – 18 – 3r + r²/2 – 3r – r²/2
so the Area of blue the triangle = 18 cm²