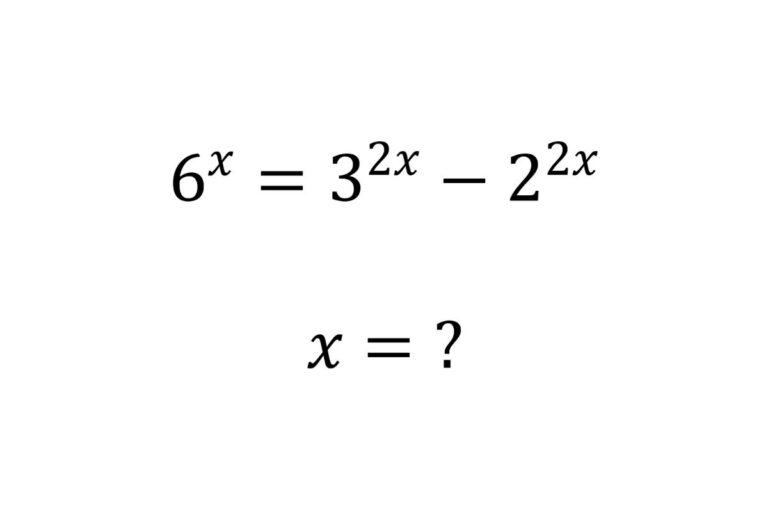
Solve the exponential equation
Solve the exponential equation 6x = 32x – 22x
The solution to the exponential equation
6x = 32x – 22x
⇒ 3x 2x = 3x 3x – 2x 2x
⇒ 1 = (3x 3x – 2x 2x)/(3x 2x)
⇒ 1 = 3x/2x – 2x/3x
⇒ 1 = (3/2)x – (2/3)x
Let a = (3/2)x then 1/a = (2/3)x
⇒ 1 = a – 1/a
⇒ a = a2 – 1
⇒ a2 – a – 1 = 0
This is a quadratic equation, so apply the quadratic formula
⇒ a = (1 ± √(1 – 4 × 1 × (-1)))/(2 × 1)
⇒ a = (1 ± √5)/2
⇒ a = (1 + √5)/2 (because (3/2)x is a real value)
Take logarithms on both sides
log (3/2)x = log ((1 + √5)/2)
⇒ x log (3/2) = log (1 + √5) – log 2
⇒ x = (log (1 + √5) – log 2)/(log 3 – log 2)