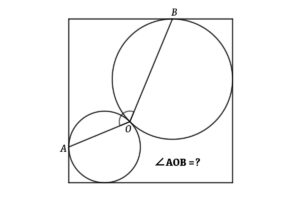
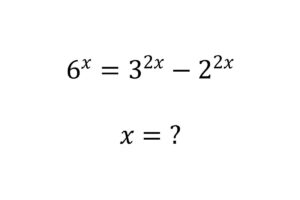Find the length of the chord
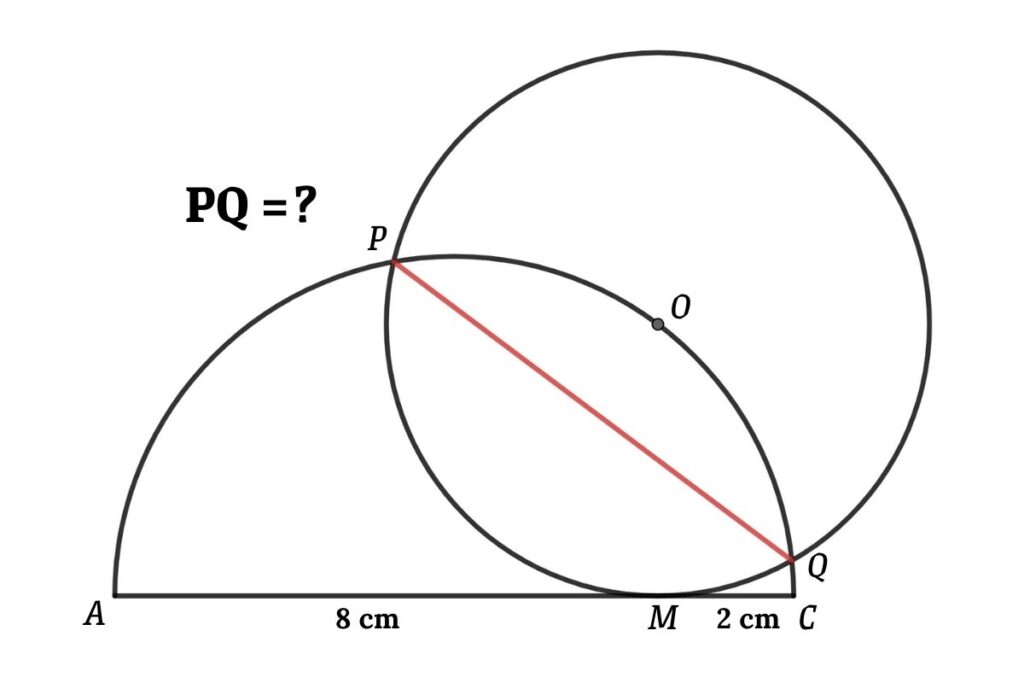
Find the length of the chord from the figure, If PQ is the common chord of the semicircle and circle
AC is the center of the semicircle, AM = 8 cm, CM = 2 cm and O is the center of the circle
Solution: Length of the chord
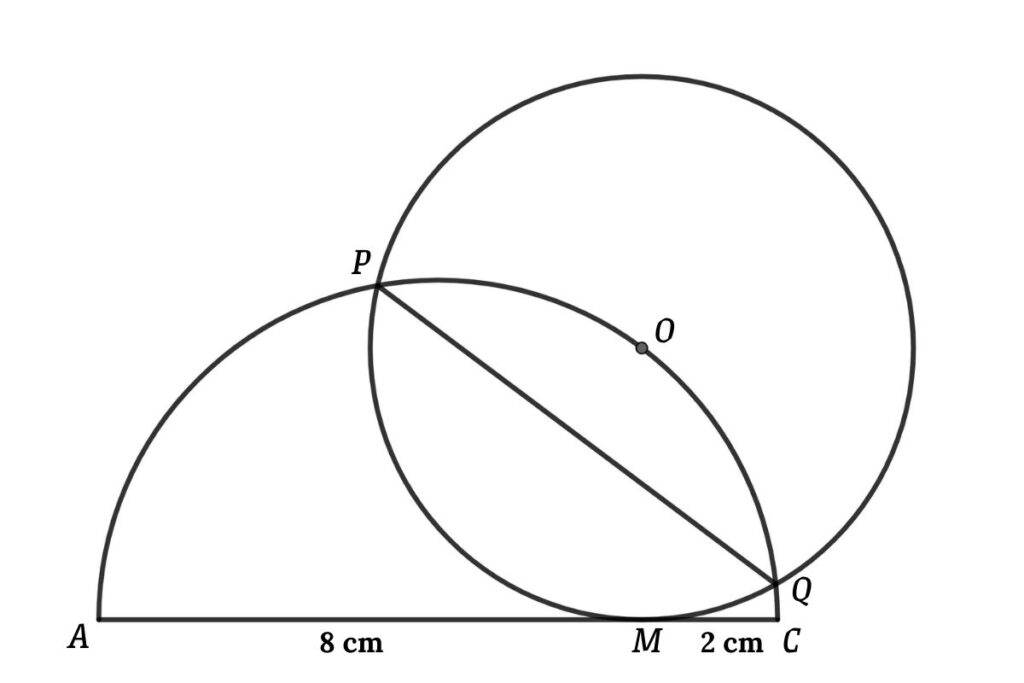
Connect OM
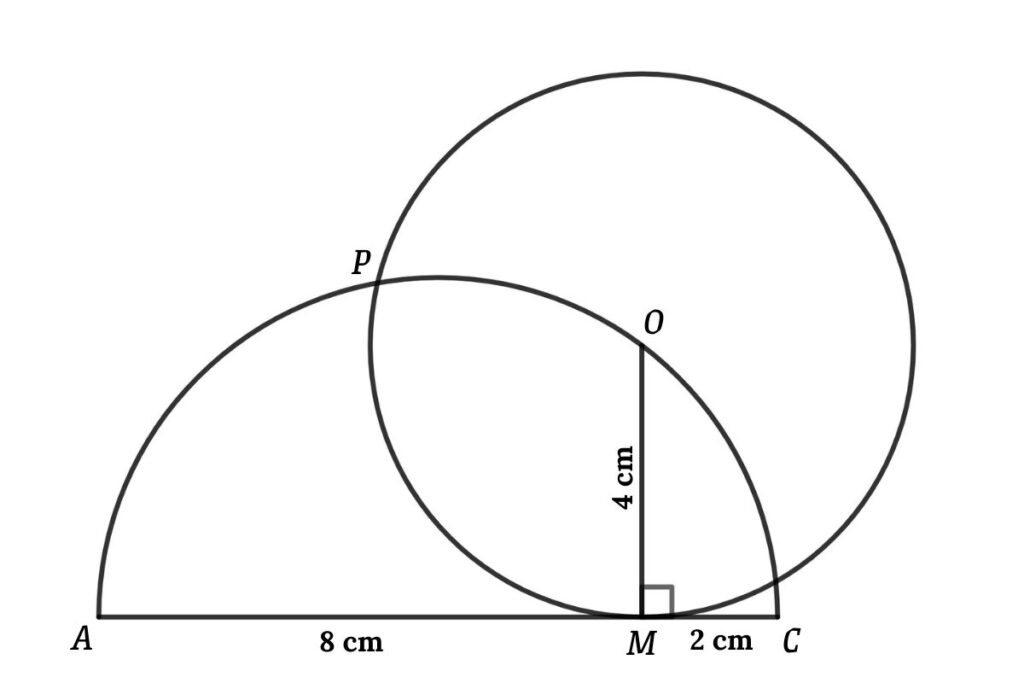
Apply the intersecting chords theorem in the figure, then
AM × CM = OM²
⇒ 8 × 2 = OM²
⇒ OM² = 16
⇒ OM = 4 cm
So we get the radius of the circle = 4 cm
Also radius of semicircle = (8 + 2) / 2 = 5 cm
Now connect OP, OB, and PB, and then we get the triangle POB
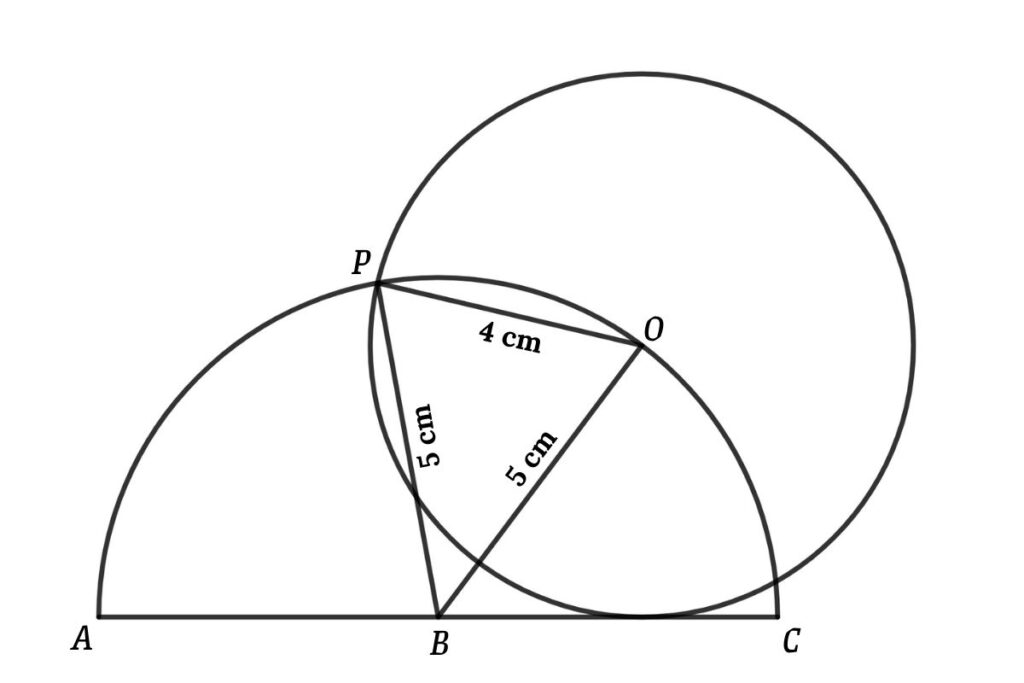
From the figure
OP = 4 cm (radius of the circle)
OB = PB = 5 cm(radius of the semicircle)
So we can find the area of the triangle POB using Heron’s formula
Area of the triangle using heron’s formula is √(s(s–a)(s–b)(s–c)
Here, s = (a + b + c) / 2, a = 5 cm, b = 5 cm and c = 4 cm
Then s = (5 + 5 + 4)/2 = 7
So area = √84 cm²
Connect PQ
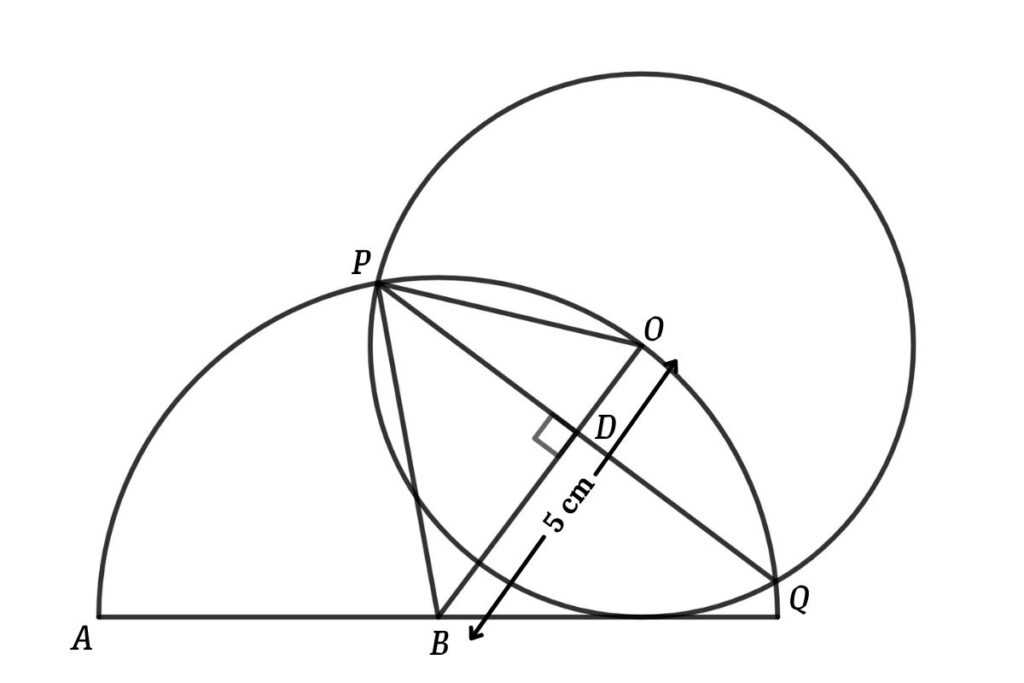
PQ is the common chord and OB connects the center of the circle and semicircle so OB is the perpendicular bisector of the chord PQ
so, PQ = 2 × PD
also, the Area of the triangle POB = ½ × OB × PD
That is, √84 = ½ × 5 × PD
So we get PD = 2√84 ÷ 5
Now, PQ = 2 × PD
That is, PQ = (8√21)/5 cm