Solve the geometry math riddle two circles are inscribed inside a square
The figure shows two circles are inscribed inside a square and when OA and OB are chords of the circles, What is the angle between the chords (∠AOB =?)
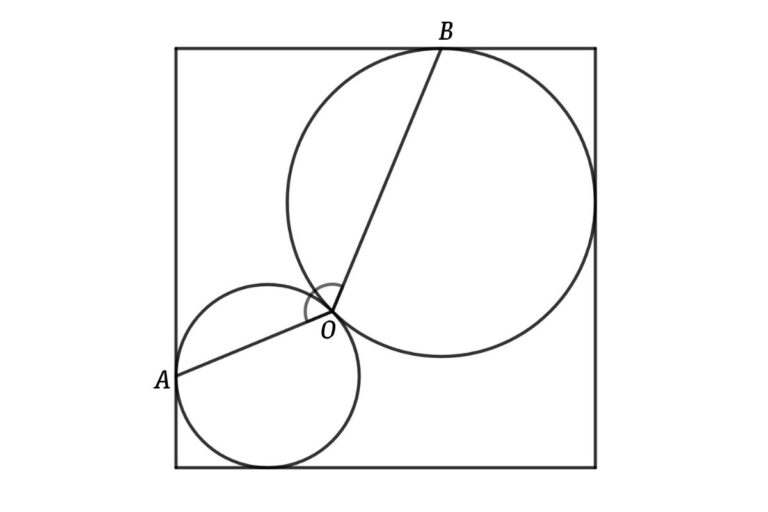
Solution
Connect the diagonal of the square, draw the diameter of the bigger circle through B, and connect the other end of the diameter to O
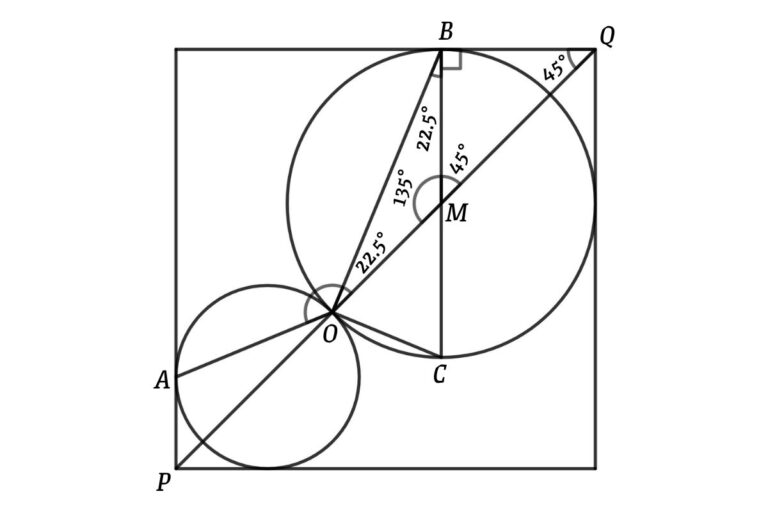
From the above figure, ΔOBC is a right angle (because BC is the diameter of the circle)
From ΔMBQ
∠MBQ = 90°
⇒ ∠BMQ = ∠BQM = (180 – 90)/2
⇒ ∠BMQ = ∠BQM = 45°
From ΔOBM
∠OMB = 180 – 45 = 135°
⇒ ∠MOB = ∠OBM = (180 – 135)/2 {MO = MB}
⇒ ∠MOB = ∠OBM = 22.5°
Now, draw the diameter of the smaller circle through A and connect the other end of the diameter to O
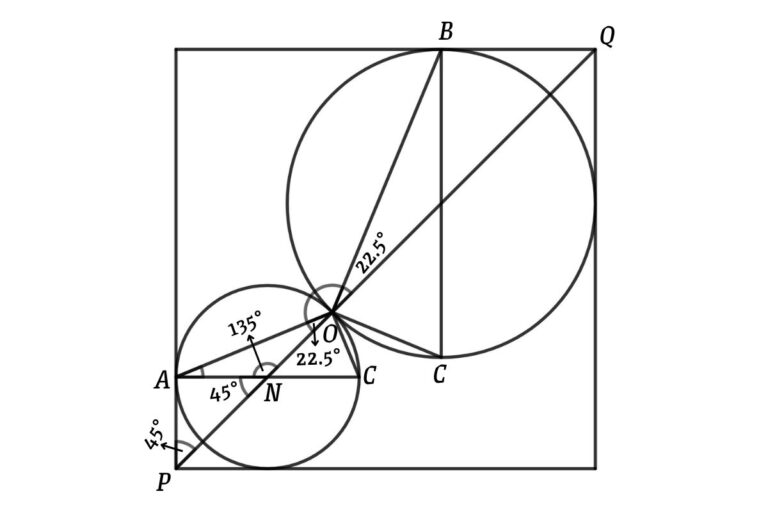
From the above figure, ΔAOC is a right angle (because AC is the diameter of the circle)
From ΔPAN
∠PAN = 90°
⇒ ∠APN = ∠ANP = (180 – 90)/2
⇒ ∠APN = ∠ANP = 45°
From ΔOAN
∠ONA = 180 – 45 = 135°
⇒ ∠AON = ∠OAN = (180 – 135)/2 {AN = ON}
⇒ ∠AON = ∠OAN = 22.5°
From figure
∠AOB = 180 – (∠AON + ∠BOQ)
⇒ ∠AOB = 180 – (22.5 + 22.5)
⇒ ∠AOB = 135°
That is, the angle between the chords is 135°