In this article, I will present algebra math problems involving the two variable systems of equations. There are numerous methods to solve a system of linear equations. Here, I am solving two variable systems of equations math problems in different methods like substitution, elimination, graphs, and matrices.
Solving the Two Variable Systems of Equations Math Problems Using Substitution
Problem 1: Solve the system of linear equations x + 2y = 8 and 3x + y = 9
Solution
Let assume
x + 2y = 8……………………………eq(1)
3x + y = 9……………………………eq(2)
From equation 1 we get
x = 8 – 2y, we can substitute the value of x in equation 2, then
3 · (8 – 2y) + y = 9
⇒ 24 – 6y + y = 9
⇒ 5y = 15
or, y = 3
Now from equation 1
x = 8 – 2y = 8 – 2 · 3 = 2
or the solution of the system of equations is x = 2 and y = 3
Problem 2: Solve the system of equations 5x + 3y = 18 and 4x + y = 13
Solution
Let assume
5x + 3y = 18………………………eq(1)
4x + y = 13………………………..eq(2)
From equation 2 we get
y = 13 – 4x, we can substitute the value of x in equation 1, then
5x + 3 · (13 – 4x) = 18
⇒ 5x + 39 – 12x = 18
⇒ 7x = 21
or, x = 3
Now from equation 2
y = 13 – 4x = 13 – 4 · 3 = 1
or the solution of the system of equations is x = 3 and y = 1
Solving the Two Variable Systems of Equations Math Problems Using Elimination
Problem 3: Solve the system of equations 4x + 3y = 31 and 3x + 2y = 22
Solution
Let assume
4x + 3y = 31………………………..eq(1)
3x + 2y = 22………………………..eq(2)
Multiply equation 1 with 2 and equation 2 with 3, then the coefficient of y becomes 6
2 · (4x + 3y) = 2 · 31
⇒ 8x + 6y = 62………………………..eq(3)
3 · (3x + 2y) = 3 · 22
⇒ 9x + 6y = 66………………………..eq(4)
Now we can eliminate y by subtracting equation 3 from equation 4
9x + 6y – (8x + 6y) = 66 – 62
⇒ x = 4
From equation 1, we get
4 · 4 + 3y = 31
⇒ 3y = 31 – 16 = 15
⇒ y = 5
or the solution of the system of equations is x = 4 and y = 5
Problem 4: Solve the system of equations 5x + 6y = 28 and 3x + 5y = 21
Solution
Let assume
5x + 6y = 28………………………..eq(1)
3x + 5y = 21………………………..eq(2)
Multiply equation 1 with 3 and equation 2 with 5, then the coefficient of x becomes 15
3 · (5x + 6y) = 3 · 28
⇒ 15x + 18y = 84………………………..eq(3)
5 · (3x + 5y) = 5 · 21
⇒ 15x + 25y = 105………………………..eq(4)
Now we can eliminate x by subtracting equation 3 from equation 4
15x + 25y – (15x + 18y) = 105 – 84
⇒ 7y = 21
⇒ y = 3
From equation 1, we get
5x + 6 · 3 = 28
⇒ 5x = 28 – 18 = 10
⇒ x = 2
or the solution of the system of equations is x = 2 and y = 3
Solving the Two Variable Systems of Equations Math Problems Using Graphs
Problem 5: Solve the system of equations x + 2y = 5 and x – 2y = 1
Solution
We will plot the graphs of x + 2y = 5 and x – 2y = 1 to solve the equation
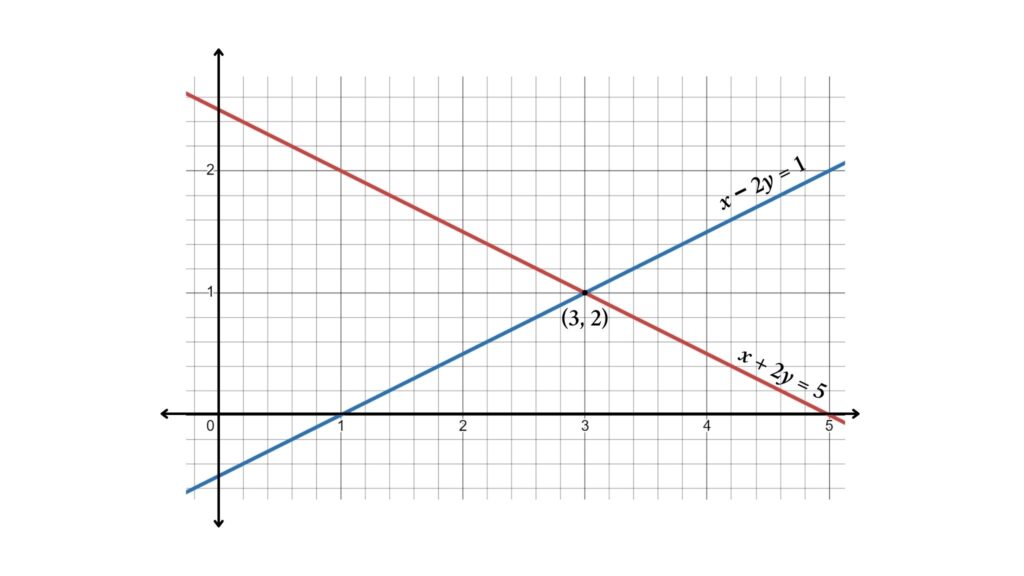
Here x + 2y = 5 and x – 2y = 1 intersecting at (3, 2) so the solution of the system of equation is x = 3 and y = 2
Problem 6: Solve the system of equations 3x + y = 8 and 2x – 3y = -2
Solution
We will plot the graphs of 3x + y = 8 and 2x – 3y = -2 to solve the equation
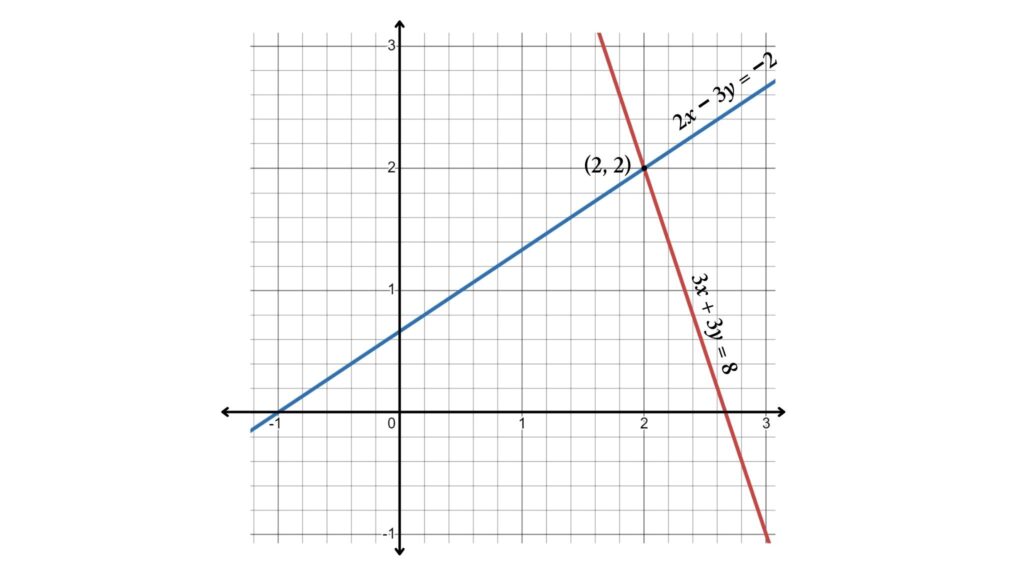
Here 3x + y = 8 and 2x – 3y = -2 intersecting at (2, 2) so the solution of the system of equation is x = 2 and y = 2
Solving the Two Variable Systems of Equations Math Problems Using Matrices
Problem 7: Solve the system of equations 2x + 3y = 1 and 6x + y = 11
Solution
Here coefficient matrix (A), variable matrix (X), and constant matrix (B) is
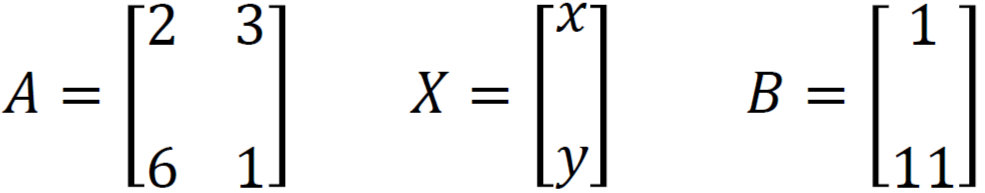
We know X = A⁻¹B, so
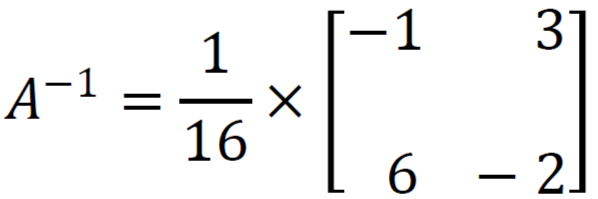
Now we get
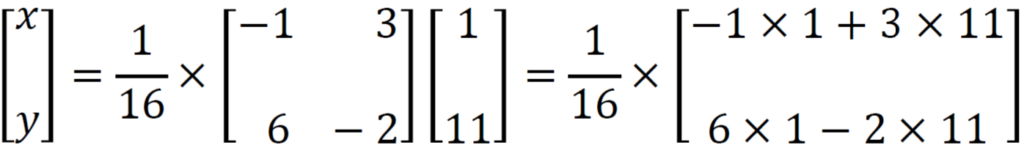
Simplify this, then we get
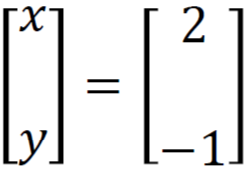
So the solutions are x = 2 and y = -1
Problem 8: Solve the system of equations 3x + y = 1 and x + 2y = -3
Solution
Here coefficient matrix (A), variable matrix (X), and constant matrix (B) is
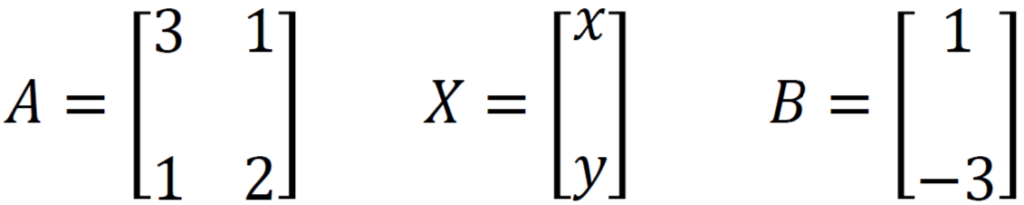
We know X = A⁻¹B, so
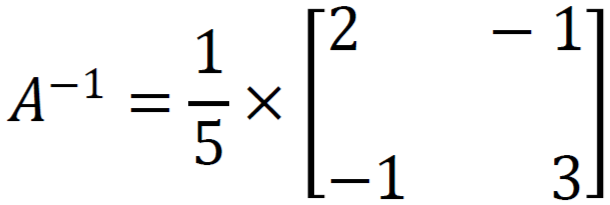
Now we get
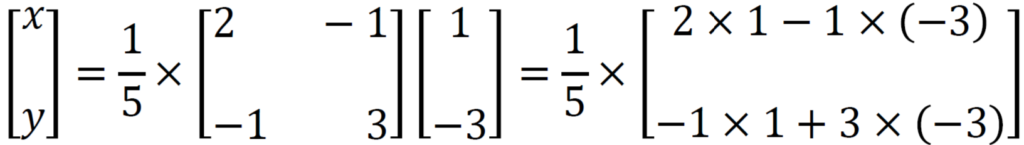
Simplify this, then we get
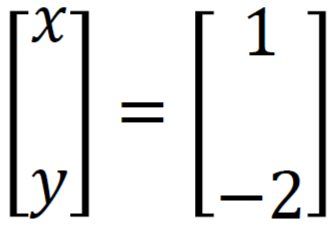
So the solutions are x = 1 and y = -2